Analyse des Relative Age Effects in internationalen Fußballturnieren: Eine Studie der Europameisterschaft 2024
Veröffentlichungsdatum: 30. Juni 2024
Abstract
Diese Studie untersucht den Relative Age Effect (RAE) während der Europameisterschaft 2024 in Deutschland, einem hochkompetitiven internationalen Fußballturnier. Der RAE beschreibt, wie ältere Spieler innerhalb eines Jahrgangs durch ihre physische und psychologische Reife systematische Vorteile in der sportlichen Selektion und Entwicklung genießen, was signifikante Auswirkungen auf die Talentförderung und Karrierechancen hat. Durch die Analyse der Geburtsdaten aller Teilnehmer, aufgeschlüsselt nach Monaten und Tagen, wurde die Verteilung der Geburtstage im Kontext des Turniers untersucht.
Die Ergebnisse zeigen signifikante Unterschiede in der Geburtsmonatsverteilung sowohl auf globaler Ebene als auch spezifisch nach Ländern. Länder wie Deutschland, England und Spanien weisen eine Konzentration von Geburten in den ersten Monaten des Jahres auf, was auf eine starke Präsenz des RAE hindeutet, während Länder wie die Slowakei und Ungarn eine gleichmäßigere Verteilung zeigen. Die detaillierte Analyse der Geburtstage in Tageszahlen liefert tiefere Einblicke in die Selektionspraktiken und unterstreicht die Notwendigkeit, bestehende Auswahlprozesse zu überdenken.
Die Studie empfiehlt, dass Fußballakademien und sportliche Entscheidungsträger ihre Methoden überarbeiten, um allen Talenten, unabhängig von ihrem Geburtsmonat, faire Entwicklungschancen zu bieten. Es wird weiterhin vorgeschlagen, die Forschung über den RAE auszuweiten, um dessen langfristige Auswirkungen auf die Karriereentwicklung von Spielern besser zu verstehen und effektive Gegenstrategien zu entwickeln. Die Ergebnisse dieser Untersuchung tragen dazu bei, die Praktiken in der Jugendfußballförderung weltweit zu verbessern und eine gerechtere Talententwicklung zu fördern.
Keyword: Talententwicklung, Relative Age Effect, Selektionskriterien, Sportstatistik
Disclaimer zur Studie
Diese Studie basiert ausschließlich auf Daten, die öffentlich zugänglich sind und keine sensiblen persönlichen Informationen enthalten. Alle Analysen und Schlussfolgerungen wurden mit größter Sorgfalt und nach bestem Wissen und Gewissen durchgeführt, basieren jedoch auf den Daten, die durch die Plattformen UEFA.com und Transfermarkt.de zur Verfügung gestellt wurden. Es wird keine Verantwortung für eventuelle Ungenauigkeiten oder Unvollständigkeiten dieser externen Datenquellen übernommen. Zudem sind die in dieser Studie gezogenen Schlussfolgerungen Interpretationen der Autoren und spiegeln nicht notwendigerweise die Ansichten oder offiziellen Positionen von foomla wider.
Die Ergebnisse dieser Untersuchung sollen zur wissenschaftlichen Diskussion und weiteren Forschung anregen, dürfen jedoch nicht als definitive Beweise für individuelle Fälle oder spezifische Situationen angesehen werden. Die Interpretationen und Empfehlungen basieren auf statistischen Durchschnittswerten und müssen im Kontext weiterer umfassender Studien betrachtet werden, um ihre Gültigkeit und Anwendbarkeit in spezifischen Fällen zu überprüfen.
1 Einleitung
Untersuchung des Relative Age Effects (RAE) bei der Europameisterschaft 2024
Die Europameisterschaft 2024 in Deutschland, die heute mit den Achtelfinalspielen beginnt, präsentiert sich nicht nur als Schauplatz für Europas Fußballelite, sondern auch als einzigartiges Forschungsfeld für die Entwicklungsmechanismen im Profisport. Ein zentrales Forschungsinteresse dieser Studie richtet sich auf den Relative Age Effect (RAE), ein Phänomen, das beschreibt, wie ältere Spieler innerhalb eines Jahrgangs systematische Vorteile in sportlicher Selektion und Entwicklung genießen. Diese Vorteile sind insbesondere in Jugendsportprogrammen von Bedeutung und haben weitreichende Auswirkungen auf die Talententwicklung und Fairness.
Studien in Sportarten wie Fußball, Eishockey und Leichtathletik haben wiederholt gezeigt, dass Spieler, die in den ersten Monaten des Kalenderjahres geboren wurden, bessere Chancen auf die Auswahl für Eliteprogramme haben. Diese systematischen Vorteile können die sportlichen Karrieren signifikant beeinflussen und die Wahrscheinlichkeit erhöhen, dass diese Athleten auf höchstem Niveau erfolgreich sind. Trotz umfangreicher Forschungen ist die spezifische Auswirkung des RAE auf Profifußballer in internationalen Turnieren noch wenig erforscht.
Die aktuelle Europameisterschaft bietet eine seltene Gelegenheit, den RAE unter den Bedingungen eines hochkompetitiven internationalen Turniers zu untersuchen und Muster sowie Trends zu identifizieren, die sonst im hektischen Turnierverlauf verborgen bleiben. Durch eine deskriptive Analyse der teilnehmenden Teams können wir nicht nur bestehende Annahmen überprüfen, sondern auch fundierte Empfehlungen für die Anpassung von Trainings- und Talentförderungsstrategien aussprechen, die zur Verbesserung der sportlichen Leistungsfähigkeit und Fairness beitragen können.
Forschungsfragen der Studie:
1. Wie verteilen sich die Geburtsmonate der Spieler über alle EM-Teilnehmer und pro Team, und welche Rückschlüsse erlaubt dies auf den Einfluss des RAE?
2. Wie unterscheidet sich die Verteilung der Geburtstage, wenn diese in Tageszahlen codiert werden, und welche tiefere Einsicht ermöglicht diese detailliertere Betrachtung?
3. Wie gestalten sich die Geburtsdatenverteilungen in den Teams, die das Achtelfinale erreicht haben, und welche Unterschiede ergeben sich aus den Lagemaßen Median und Mittelwert?
2 Methodik
Datenerhebung und Analyseverfahren zur Erforschung des RAE
Datenerhebung
Die Datenerhebung für diese Studie erfolgte hauptsächlich über UEFA.com, ergänzt durch Daten von Transfermarkt.de. Beide Plattformen sind renommiert für ihre umfassenden Datenbanken, die präzise Informationen zu Geburtsdaten, Karrierestatistiken und Teilnahmen an internationalen Turnieren bieten. Insbesondere wurden die offiziellen Turnierstatistiken und Teamzusammenstellungen der Europameisterschaft 2024 von UEFA.com entnommen. Ein Abgleich dieser Informationen mit den Einträgen auf Transfermarkt.de ermöglichte es, die Genauigkeit und Vollständigkeit der Daten zu verifizieren und potenzielle Diskrepanzen zu identifizieren und zu korrigieren, was zur Zuverlässigkeit der Studienergebnisse beiträgt.
Datenanalyse
Die Analyse der gesammelten Daten wurde in mehreren Schritten durchgeführt, die detailliert im R-Code dokumentiert sind (siehe Anhang). Initial wurde eine gründliche Datenbereinigung vorgenommen, um Datumsangaben zu standardisieren und inkonsistente oder fehlende Einträge zu bereinigen. Anschließend erfolgte die Berechnung deskriptiver Statistiken, um ein klares Bild der Frequenzen und Verteilungen der Geburtsmonate und Altersklassen der Spieler zu erhalten. Diese Analysen bildeten die Grundlage für die weiteren Untersuchungen.
Zur tiefergehenden Analyse wurden zentrale Lagemaße wie Mittelwert, Median und Modus bestimmt. Dies ermöglichte eine umfassende Betrachtung der zentralen Tendenz der Geburtsdaten. Komplementär dazu kamen verschiedene Visualisierungstechniken zum Einsatz, darunter Barplots zur Veranschaulichung der Frequenzverteilungen und Boxplots zur Darstellung der Datenverteilungen und zur Identifizierung von Ausreißern. Diese visuellen Darstellungen erleichtern das Verständnis des Einflusses des Geburtsmonats auf die Spielerselektion und -leistung.
Verwendete Bibliotheken
Die Analysen wurden mit der statistischen Software R durchgeführt, unter Einsatz spezifischer Pakete wie `dplyr`, `ggplot2` und `lubridate` zur Datenmanipulation und grafischen Darstellung. Um die Reproduzierbarkeit der Studienergebnisse zu gewährleisten, wird der vollständige Analysecode im Anhang des Artikels bereitgestellt.
Ethik und Genehmigungen
Die Studie verwendet ausschließlich Daten aus öffentlich zugänglichen Quellen, die keine sensiblen persönlichen Informationen enthalten, wodurch die Einhaltung datenschutzrechtlicher Bestimmungen gewährleistet wird.
3 Ergebnisse:
Detaillierte Ergebnisanalyse des Relative Age Effects bei der EM 2024
3.1 Ergebnisse der ersten Forschungsfrage: Häufigkeitsverteilung der Geburtsmonate
3.1.1 Globale Verteilung aller EM-Spieler
Die Analyse der Geburtsmonatsverteilungen offenbart signifikante Unterschiede in der Anzahl der Geburten pro Monat, was auf den Einfluss des Relative Age Effect (RAE) hindeuten könnte. Besonders auffällig ist die erhöhte Anzahl von Geburten in den Monaten Februar (76) und Mai (72), verglichen mit Monaten wie Juli (45) und Dezember (32), was darauf hinweisen könnte, dass Spieler, die in den ersten Monaten des Jahres geboren wurden, aufgrund von Altersvorteilen bevorzugt in Fußballakademien aufgenommen werden. Andere Monate wie März (61), Juni (49) und September (43) zeigen eine moderatere Verteilung, was darauf hindeutet, dass der Einfluss des RAE in diesen Zeiten möglicherweise weniger ausgeprägt ist.
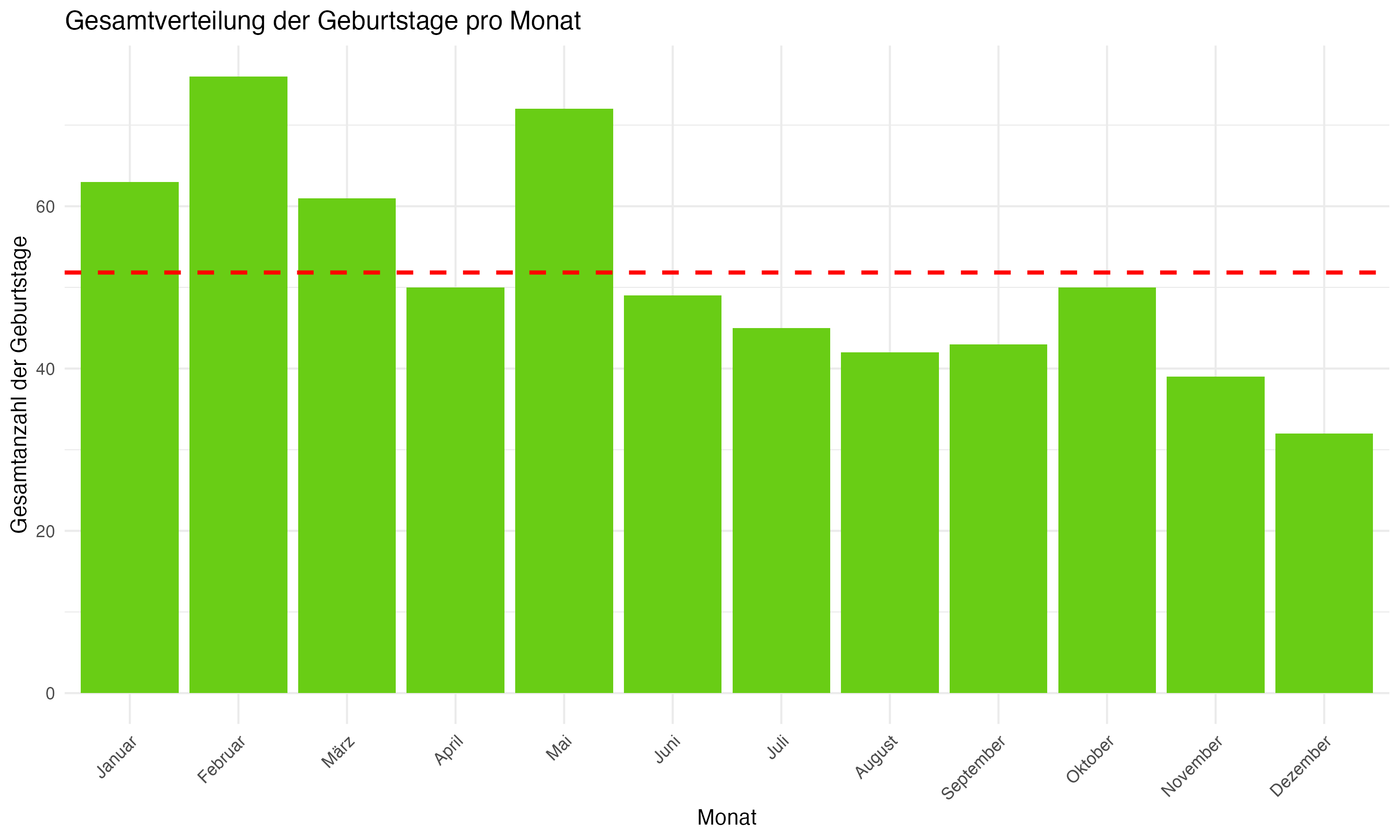
Tabelle: Absolute Häufigkeiten der Geburtsmonate aller teilnehmenden EM-Fußballer (N = 623)
Monat | n | Monat | n |
Januar | 63 | Juli | 45 |
Februar | 76 | August | 42 |
März | 61 | September | 43 |
April | 50 | Oktober | 50 |
Mai | 72 | November | 39 |
3.1.2 Team-spezifische Verteilung
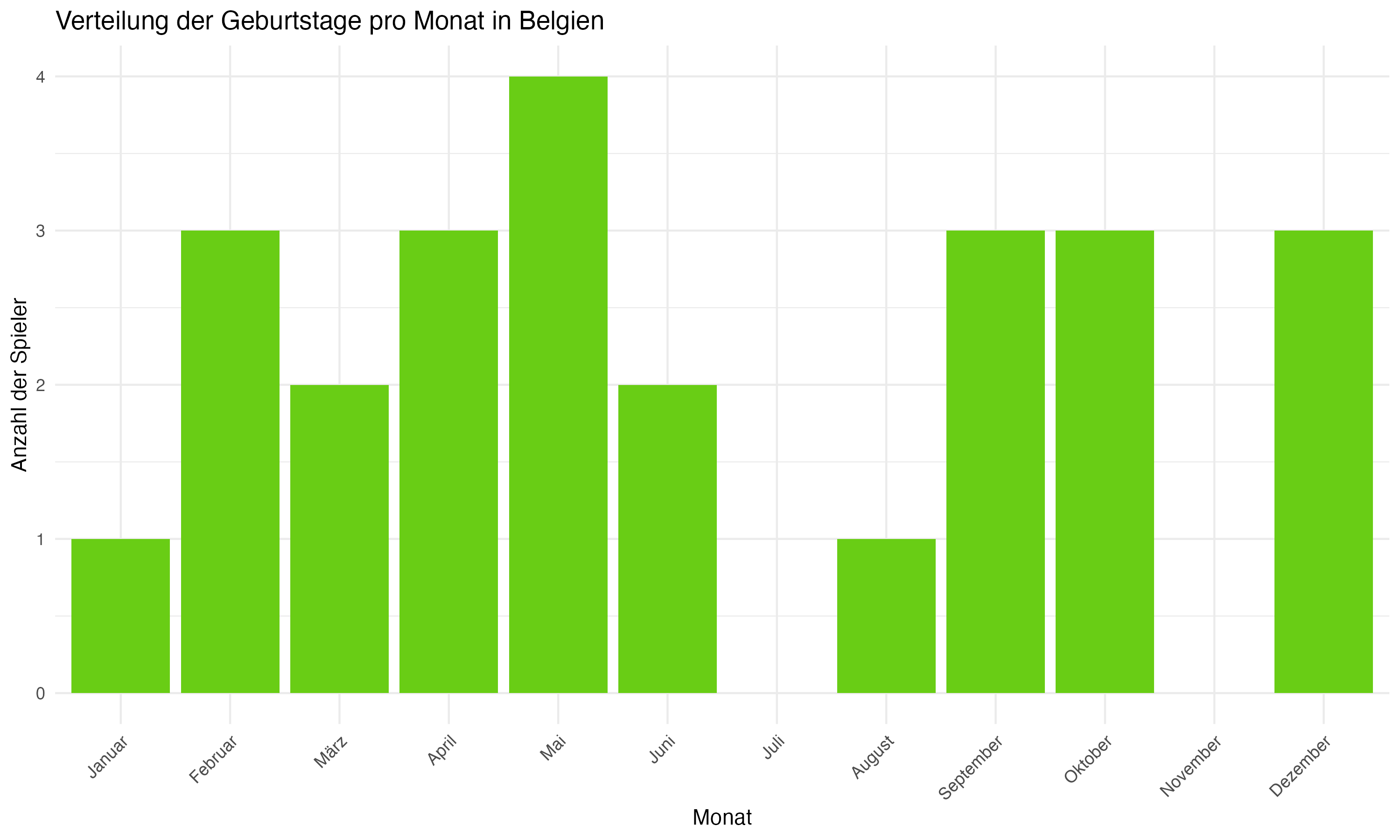
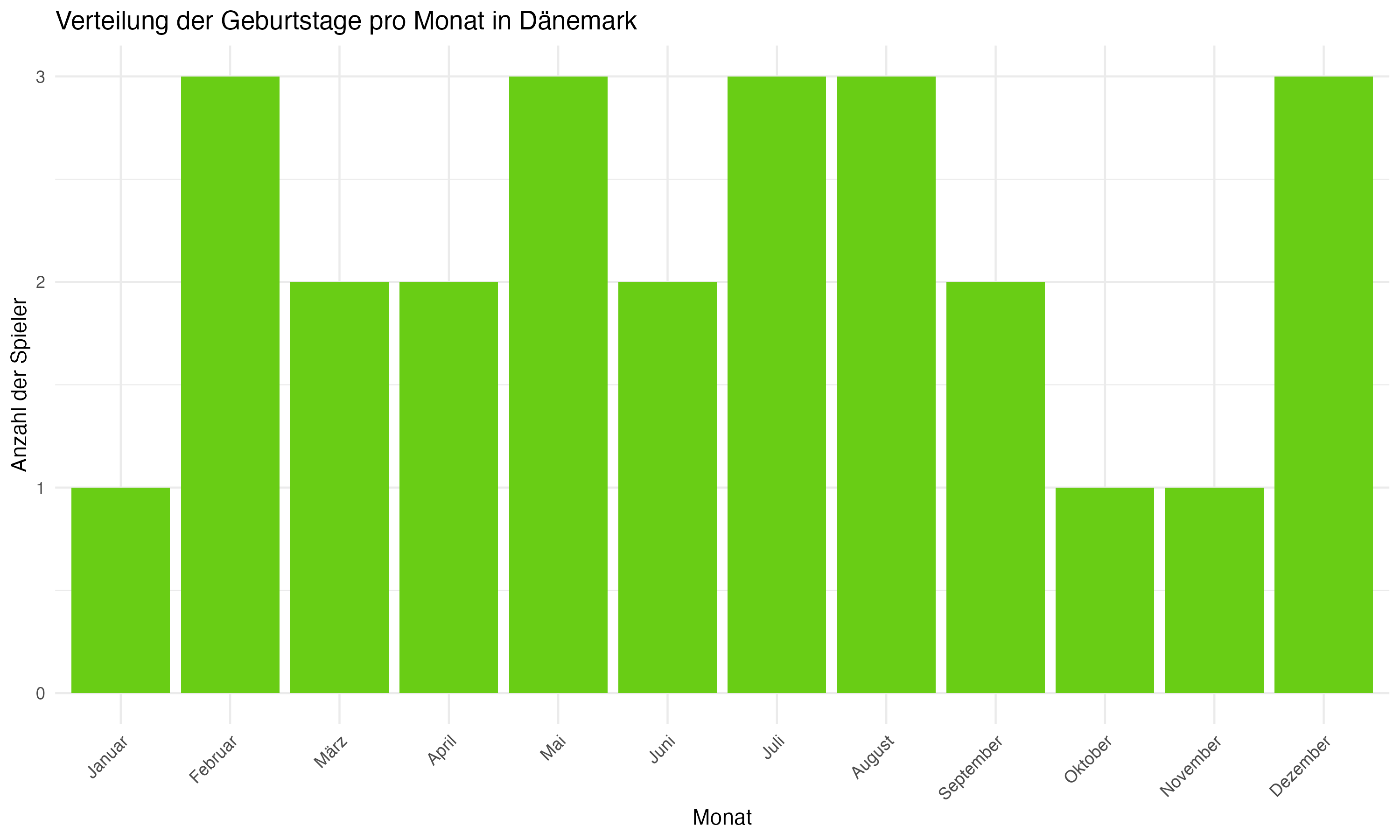
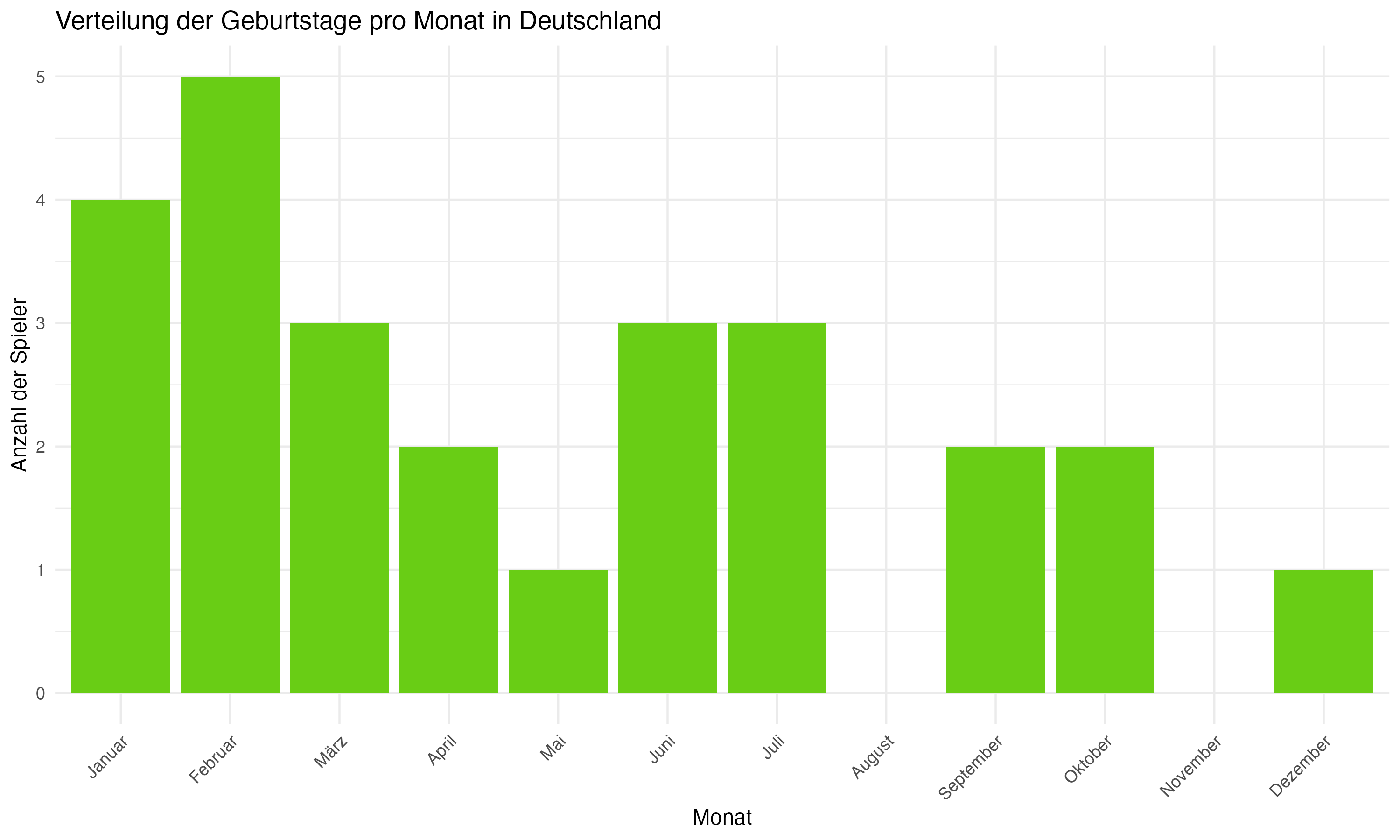
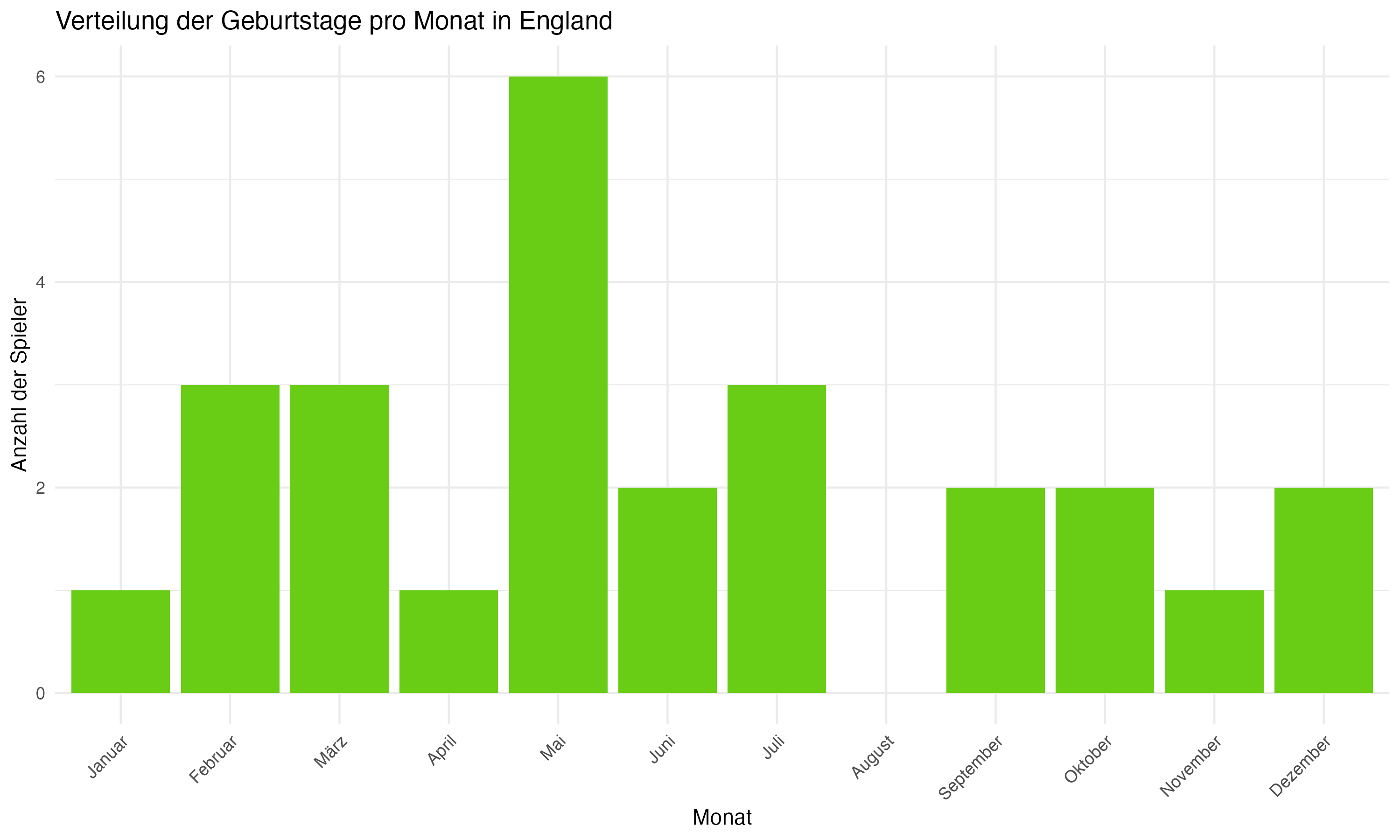
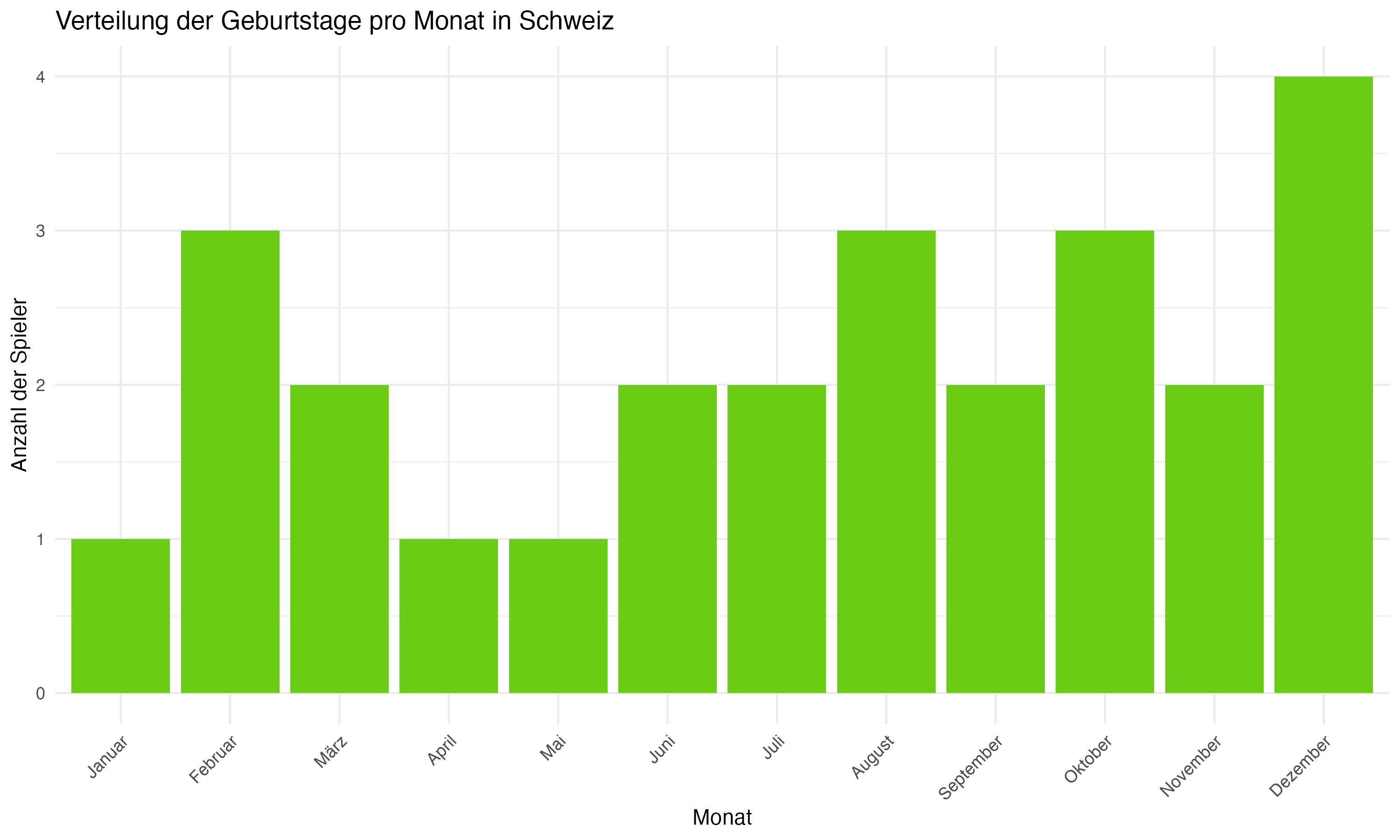
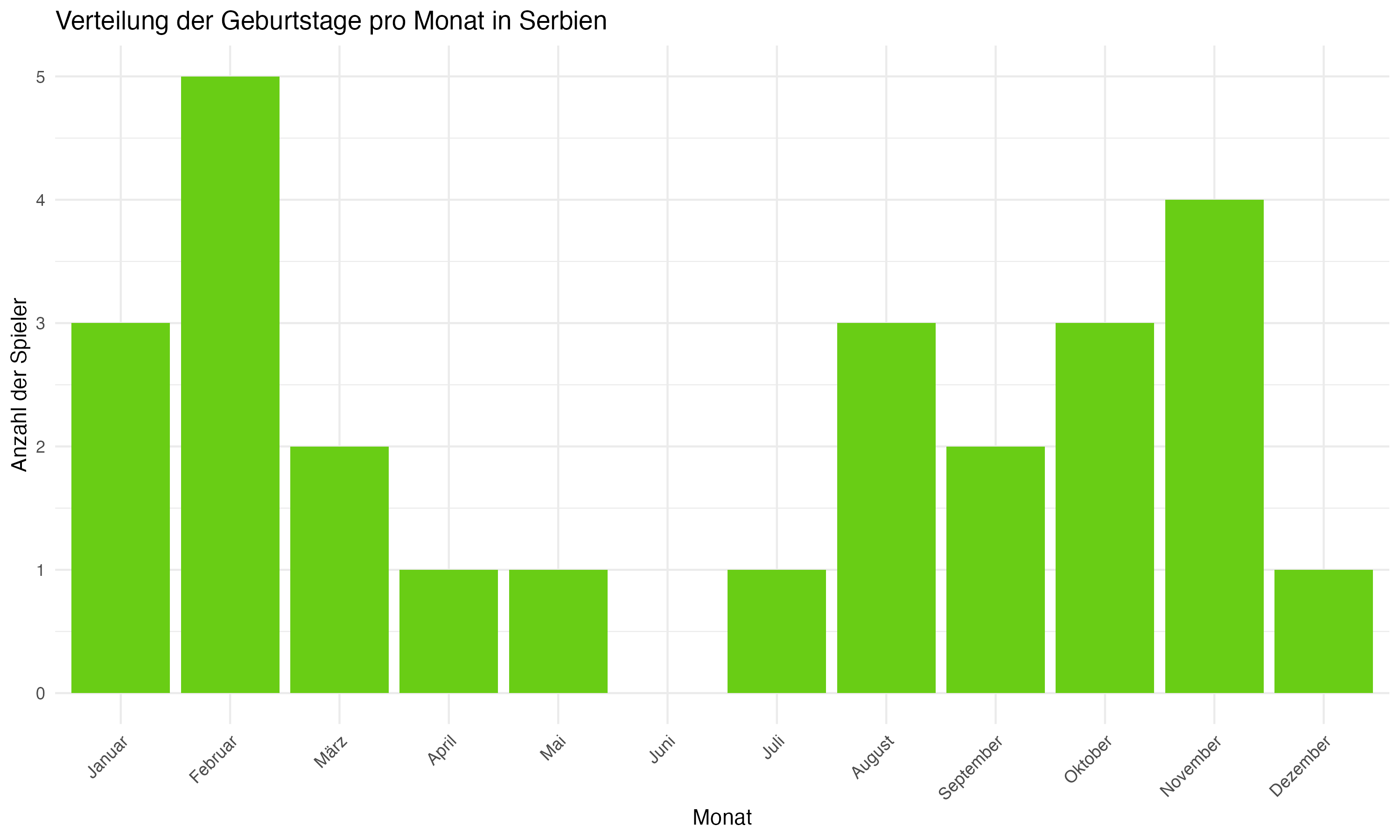
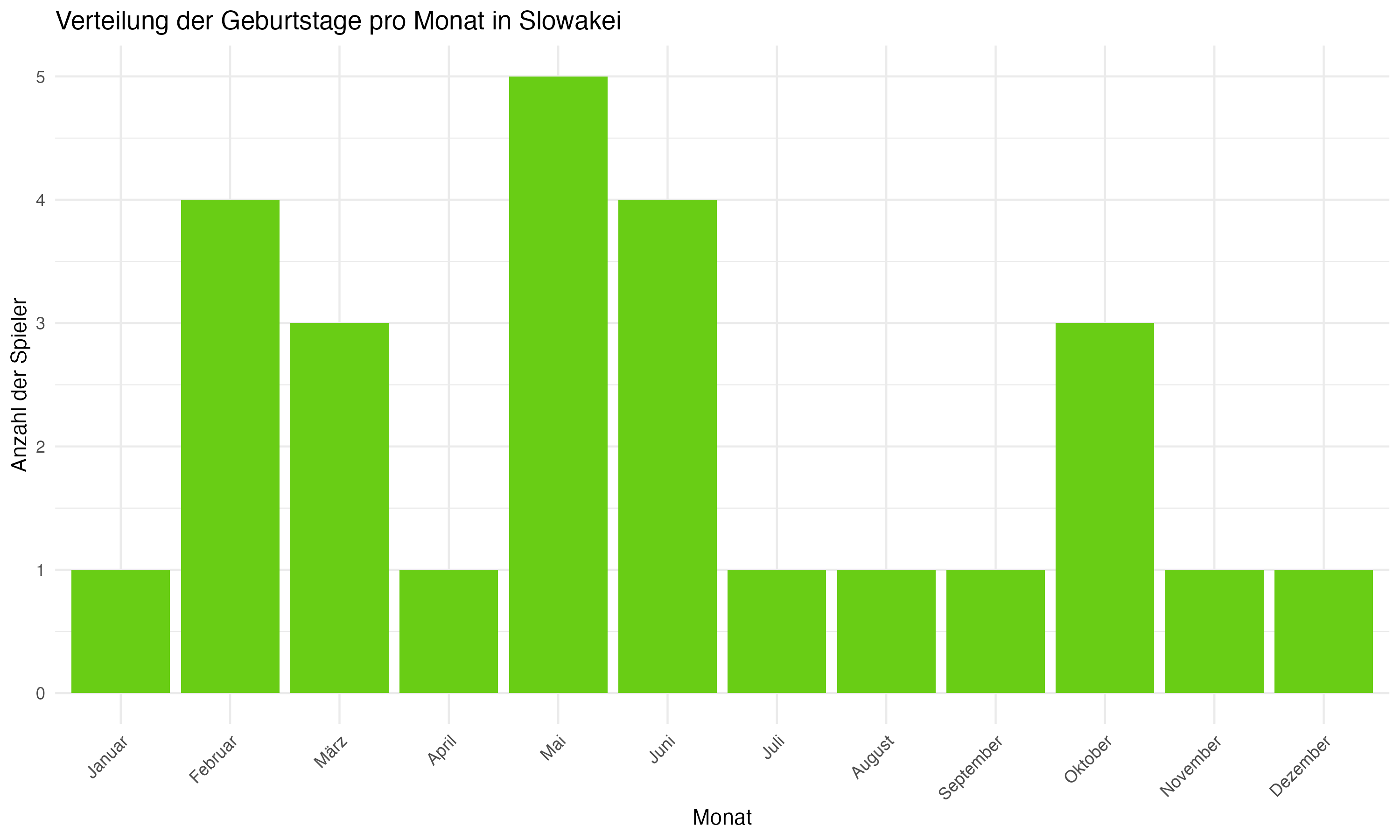
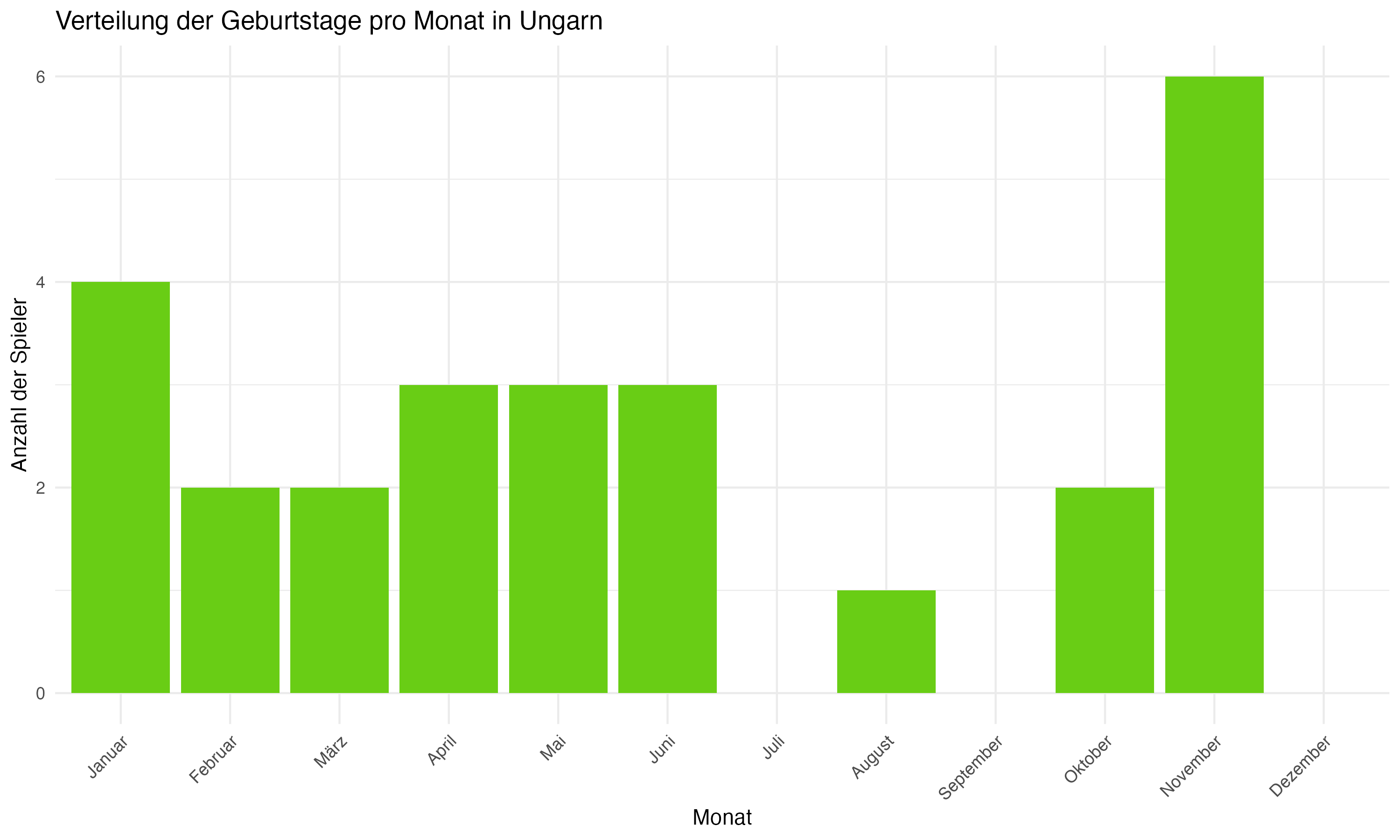
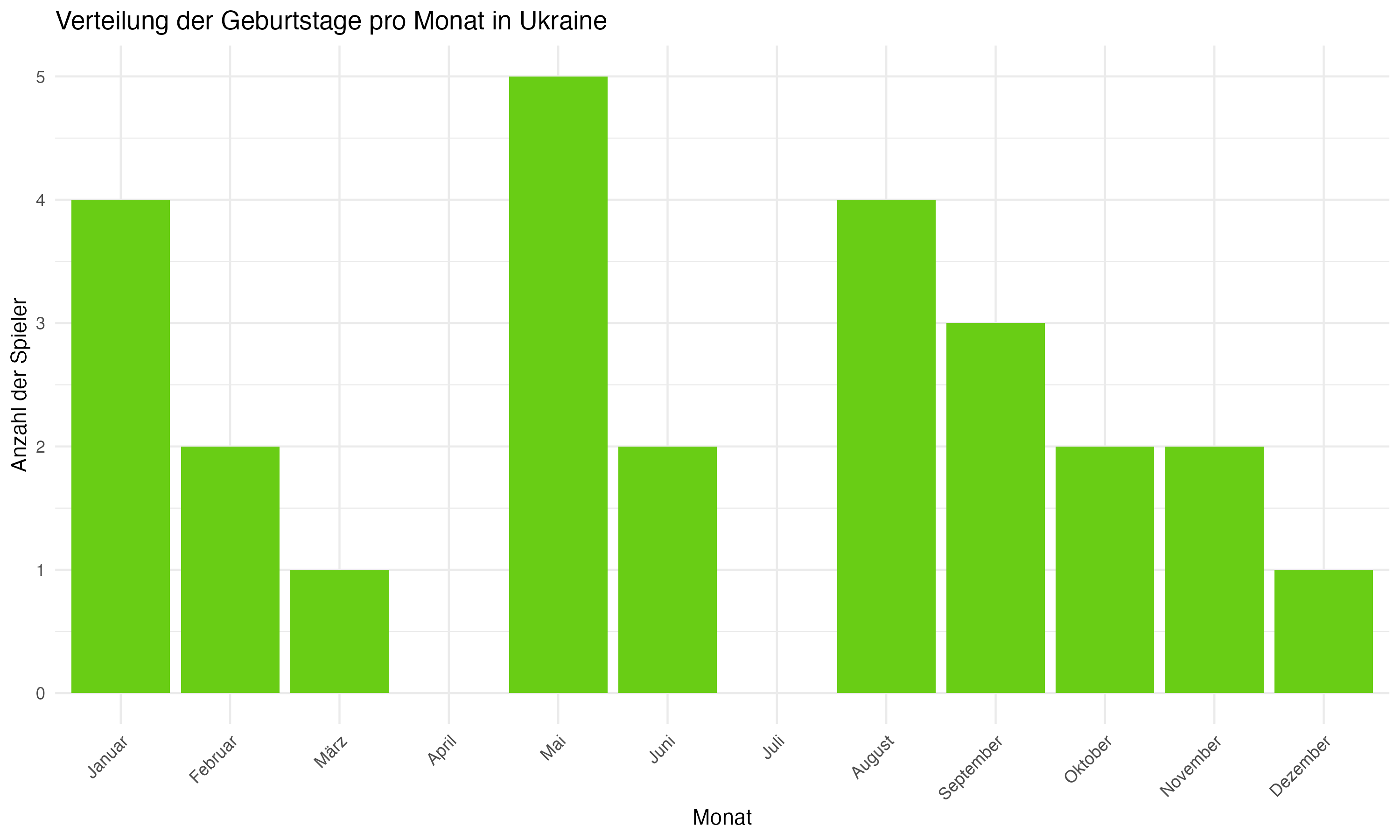
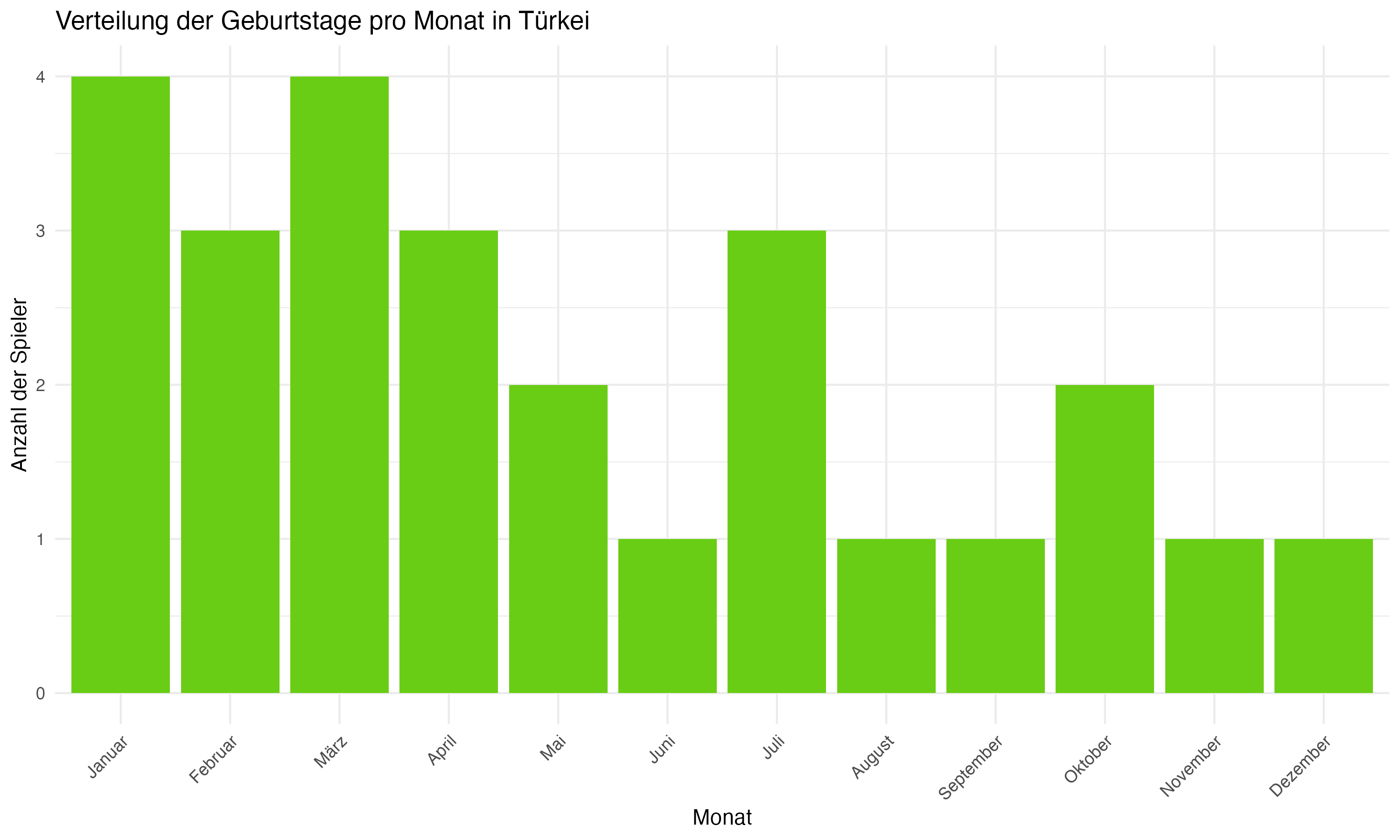
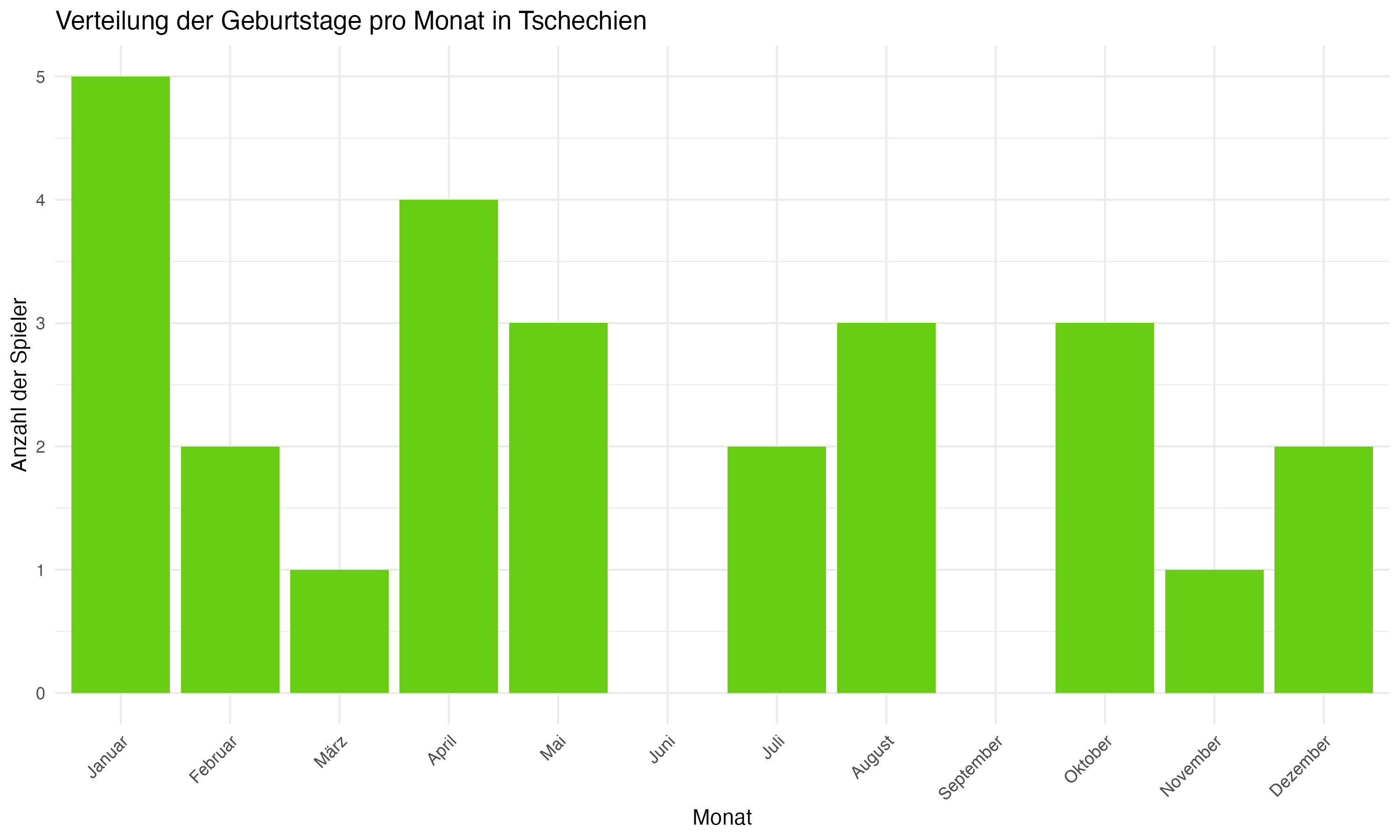
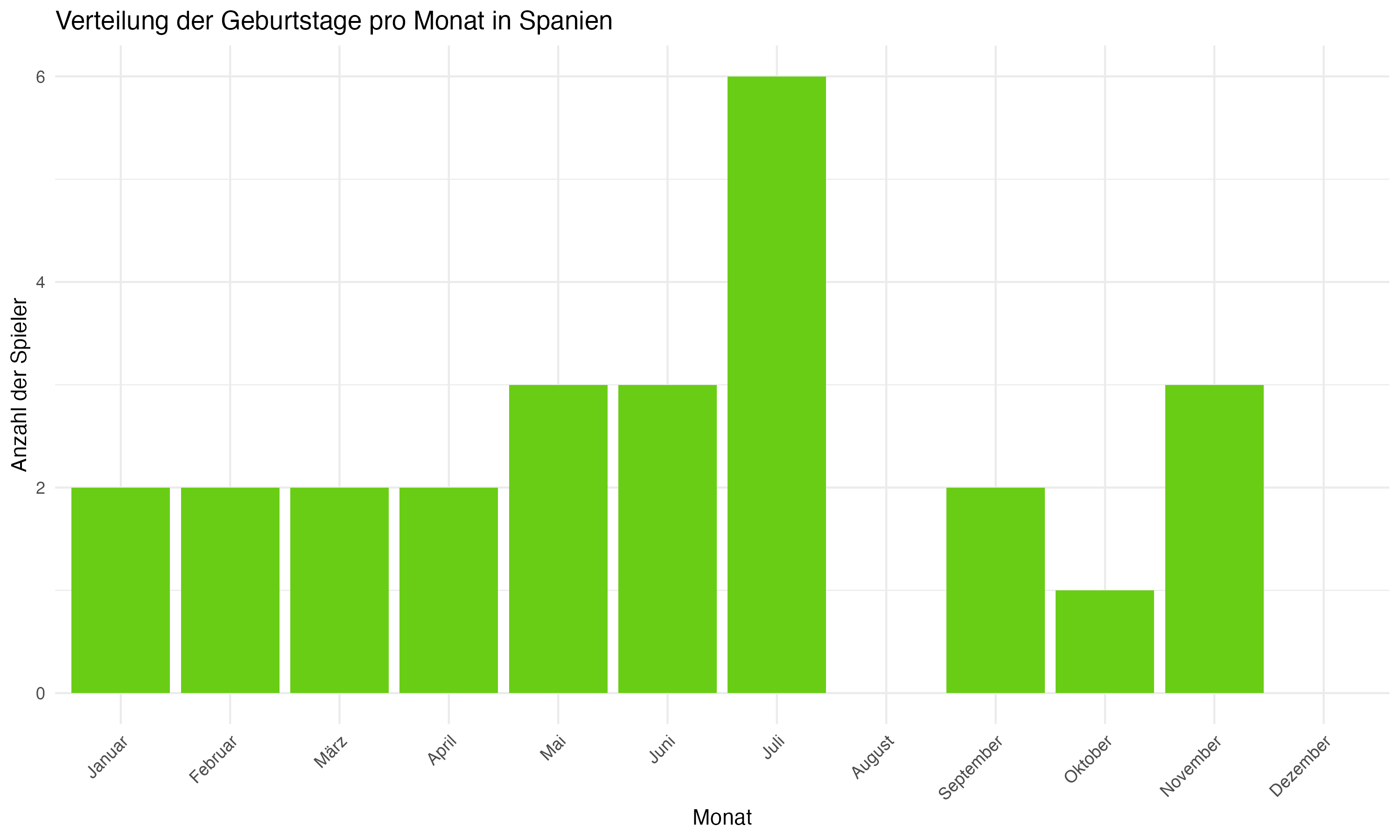
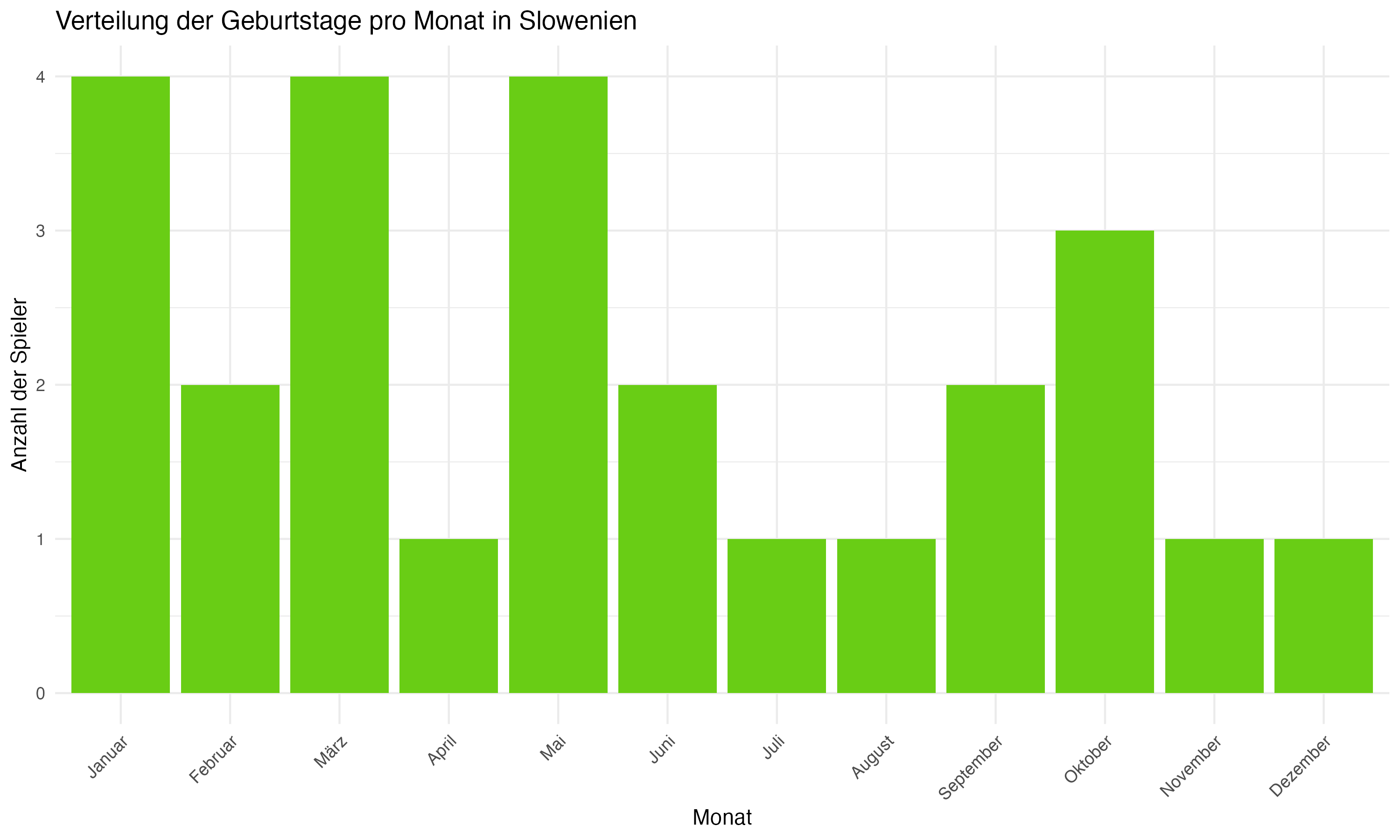
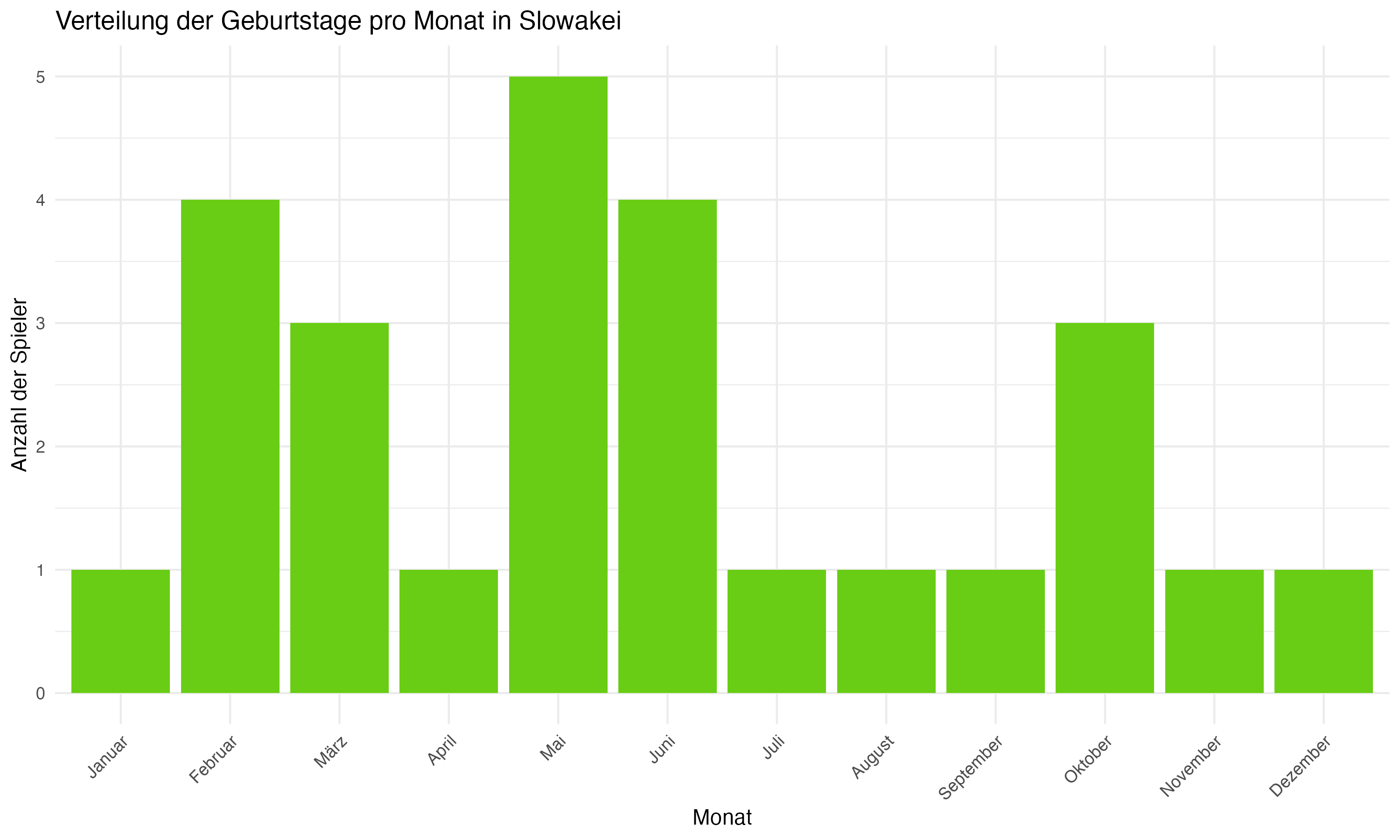
Die team-spezifische Analyse der Geburtsmonatsverteilungen zeigt signifikante Unterschiede zwischen den Mannschaften. Länder wie Deutschland, England und Spanien weisen eine deutliche Konzentration von Geburtstagen in den ersten Monaten des Jahres auf, was auf eine starke Präsenz des RAE hindeutet. Im Gegensatz dazu zeigen Länder wie die Slowakei und Ungarn eine gleichmäßigere Verteilung, die möglicherweise auf unterschiedliche Auswahlkriterien oder eine geringere Ausprägung des RAE hinweist.

Tabelle 1: Häufigkeitstabelle Geburtsmonate pro Team
3.2 Ergebnisse der zweiten Forschungsfrage: Detaillierte Verteilung der Geburtstage
3.2.1 Globale Verteilung aller EM-Spieler
Die detaillierte statistische Analyse der Geburtstage aller Teilnehmer (N = 623) zeigt eine Verteilung, die das gesamte Kalenderjahr umfasst. Der Median liegt am 148. Tag (Mitte Mai), während der Mittelwert etwas später bei 161 Tagen liegt, was eine leichte Rechtsschiefe in der Verteilung anzeigt. Die Daten reichen vom 1. bis zum 364. Tag des Jahres, was die vollständige Bandbreite der Geburtstage unter den Spielern verdeutlicht und darauf hindeuten könnte, dass der RAE Einfluss auf die frühe Entwicklung und Selektion der Spieler hat.
Minimum (Min.): Der früheste Geburtstag im Datensatz fällt auf den 1. Tag des Jahres, was darauf hindeutet, dass einige Spieler gleich zu Beginn des Jahres geboren wurden.
Erstes Quartil (1st Qu.): 25% der Spieler haben Geburtstage, die am oder vor dem 69. Tag des Jahres liegen, was ungefähr dem Beginn März entspricht. Dies zeigt eine frühe Konzentration der Geburtstage im Kalenderjahr.
Median: Der Median der Geburtstage liegt auf dem 148.5 Tag, etwa Mitte Mai. Dies bedeutet, dass die Hälfte der Spieler vor und die andere Hälfte nach diesem Datum geboren wurde, was eine zentrale Tendenz in der Mitte des zweiten Quartals anzeigt.
Durchschnitt (Mean): Der Durchschnittswert der Geburtstage liegt bei 161 Tagen, was ebenfalls ungefähr Mitte Juni entspricht. Der Mittelwert liegt etwas später als der Median, was auf eine leichte Rechtsschiefe in der Verteilung hinweist.
Drittes Quartil (3rd Qu.): 75% der Spieler haben Geburtstage, die am oder vor dem 251. Tag des Jahres, etwa Anfang September, liegen. Dies zeigt, dass die meisten Geburtstage innerhalb der ersten drei Quartale des Jahres konzentriert sind.
Maximum (Max.): Das späteste Geburtsdatum im Datensatz fällt auf den 364. Tag des Jahres, nahezu das Ende des Jahres, was die vollständige Bandbreite der möglichen Geburtstage unter den Spielern verdeutlicht.
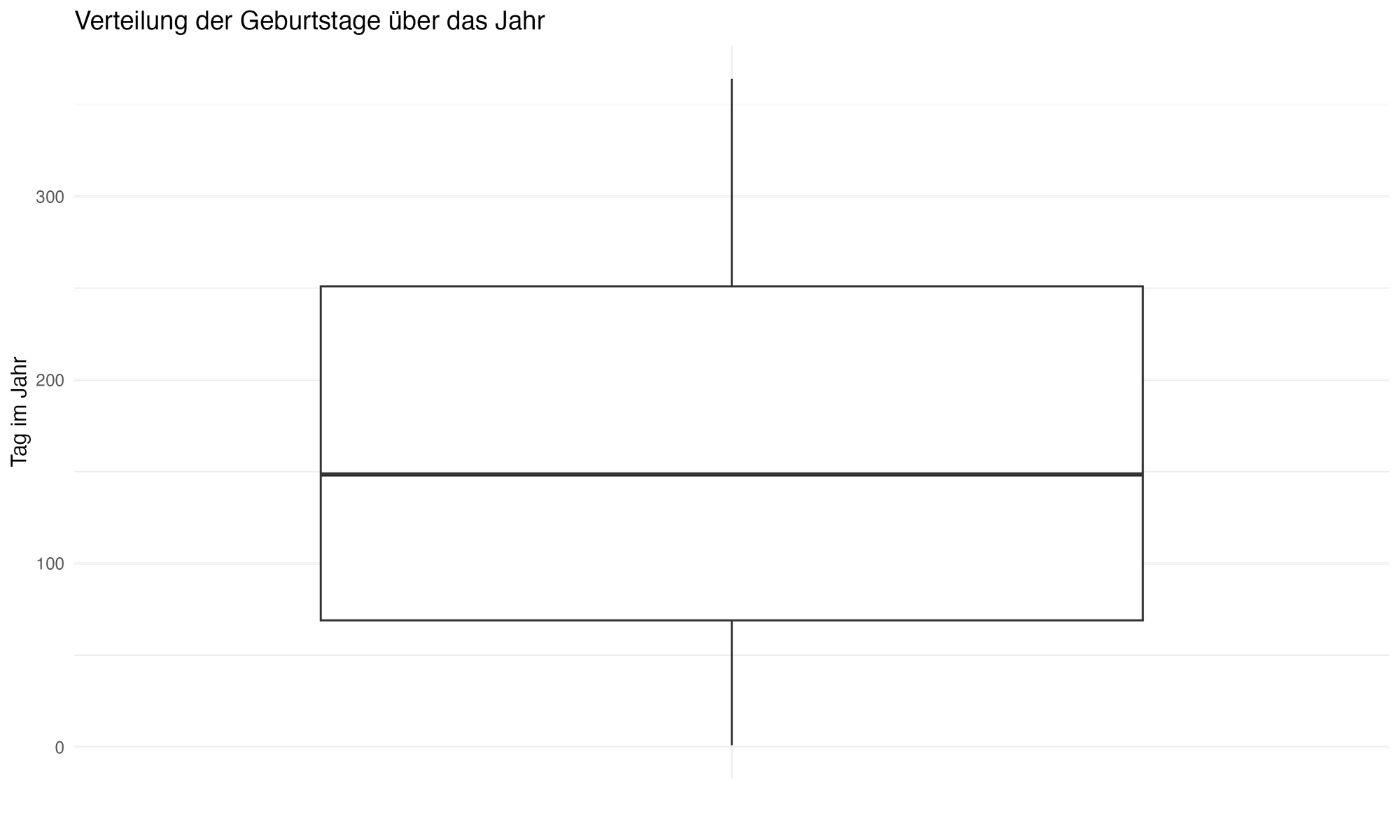
Minimum | 1st Quartil | Median | Mittelwert | 3rd Quartil | Maximum |
1.0 | 69.0 | 148.5 | 161.0 | 251.0 | 364.0 |
3.2.2 Länderspezifische Verteilung aller EM-Spieler
Die Transformation der Geburtsdaten in Tageszahlen ermöglicht eine präzisere Analyse der Verteilung. Diese Methode verdeutlicht, wie Geburtstage über das Jahr verteilt sind und liefert tiefere Einblicke in die potenziellen Auswirkungen des RAE. Die Ergebnisse für jedes Land werden in einer interaktiven Tabelle dargestellt, die es ermöglicht, spezifische Muster und Anomalien zu erkennen.

Tabelle 2: Lagemaße der Geburtstage pro Team
3.3 Individualanalysen der Teams im Achtelfinale
In diesem Abschnitt konzentriert sich die Forschung auf die detaillierte Untersuchung der Ergebnisse aus verschiedenen Ländern. Diese Analyse zielt darauf ab, spezifische Einblicke in die Geburtsdatenverteilung der Teams zu gewinnen, die das Achtelfinale erreicht haben.
3.3.1 Individualanalyse Schweiz
Detaillierte Ergebnisse für die Schweiz:
· Minimum: 6 Tage
· Unteres Quartil: 115.75 Tage
· Median: 223 Tage
· Oberes Quartil: 295 Tage
· Maximum: 354 Tage
· Mittelwert: 207 Tage
· Standardabweichung: 110.63 Tage
· Differenz zwischen Mittelwert und Median: -16 Tage
Analyse
1. Verteilung der Geburtsdaten:
Der Median von 223 Tagen, was in etwa Ende Juli entspricht, deutet darauf hin, dass mehr als die Hälfte der Schweizer Spieler in der zweiten Hälfte des Jahres geboren wird. Dies steht im Gegensatz zu der oft in Fußballakademien beobachteten Tendenz, dass viele Spieler aus sportlich erfolgreichen Ländern tendenziell in den ersten Monaten des Jahres geboren werden.
Der Mittelwert liegt bei 207 Tagen, ungefähr Mitte Juli, was eine breitere Streuung der Geburtsdaten nahelegt. Die negative Differenz zwischen Mittelwert und Median (-16 Tage) weist darauf hin, dass die Verteilung leicht linksschief ist, was bedeutet, dass es mehr Spieler gibt, die später im Jahr geboren wurden, verglichen mit einem symmetrischen Verteilungsmodell.
2. Quartile und Extremwerte:
Das untere Quartil bei 115.75 Tagen (ca. Ende April) und das obere Quartil bei 295 Tagen (ca. Ende Oktober) zeigen, dass 50% der Geburten zwischen April und Oktober liegen, mit einer breiten Streuung der Geburtstage über das Jahr.
Das Minimum von 6 Tagen und das Maximum von 354 Tagen demonstrieren, dass es Spieler gibt, die fast das ganze Jahr über geboren werden, was auf eine sehr heterogene Altersstruktur innerhalb der Spielerpopulation hinweist.
3.3.2 Individualanalyse Deutschland
Detaillierte Ergebnisse für Deutschland:
· Minimum: 4 Tage
· Unteres Quartil: 45 Tage
· Median: 116.5 Tage
· Oberes Quartil: 200.5 Tage
· Maximum: 335 Tage
· Mittelwert: 129.81 Tage
· Standardabweichung: 100.22 Tage
· Differenz zwischen Mittelwert und Median: 13.31 Tage
Analyse
1. Verteilung der Geburtsdaten:
Der Median von 116.5 Tagen, der in etwa Mitte April entspricht, deutet darauf hin, dass die Mehrheit der deutschen Spieler im ersten Drittel des Jahres geboren wird. Dies ist ein typisches Zeichen für den Relative Age Effect (RAE), bei dem ältere Spieler innerhalb eines Jahrgangs aufgrund von Entwicklungs- und Reifevorteilen bevorzugt werden könnten.
Der Mittelwert liegt bei 129.81 Tagen, ebenfalls um Mitte April. Die positive Differenz zwischen Mittelwert und Median (13.31 Tage) zeigt eine leicht rechtsschiefe Verteilung an, was darauf hindeutet, dass eine signifikante Anzahl von Spielern auch später im Jahr geboren wird, obwohl der Schwerpunkt auf den früheren Monaten liegt.
2. Quartile und Extremwerte:
Das untere Quartil bei 45 Tagen (Mitte Februar) und das obere Quartil bei 200.5 Tagen (Ende Juli) zeigt, dass 50% der Geburten in einem Zeitraum von etwa fünf Monaten stattfinden, was auf eine starke Konzentration der Geburten in den ersten Monaten des Jahres hindeutet.
Das Minimum von 4 Tagen und das Maximum von 335 Tagen zeigen, dass Geburten über fast das gesamte Jahr verteilt sind, jedoch mit einer deutlichen Häufung in den ersten Monaten.
3.3.3 Individualanalyse England
Detaillierte Ergebnisse für England:
· Minimum: 14 Tage
· Unteres Quartil: 84.25 Tage
· Median: 148.50 Tage
· Oberes Quartil: 238.25 Tage
· Maximum: 364 Tage
· Mittelwert: 169.23 Tage
· Standardabweichung: 100.55 Tage
· Differenz zwischen Mittelwert und Median: 20.73 Tage
Analyse
1. Verteilung der Geburtsdaten:
Der Median von 148.5 Tagen, der etwa Mitte Mai entspricht, zeigt, dass die Hälfte der englischen Spieler in der ersten Hälfte des Jahres geboren wird. Dies deutet auf eine gewisse Präsenz des Relative Age Effects (RAE) hin, der ältere Spieler innerhalb ihres Jahrgangs bevorzugt.
Der Mittelwert liegt bei 169.23 Tagen, ungefähr Ende Juni, was auf eine breitere Streuung der Geburtsdaten hinweist. Die positive Differenz zwischen Mittelwert und Median (20.73 Tage) illustriert eine rechtsschiefe Verteilung, was bedeutet, dass eine bedeutende Anzahl von Spielern auch später im Jahr geboren wird.
2. Quartile und Extremwerte:
Das untere Quartil bei 84.25 Tagen (Ende März) und das obere Quartil bei 238.25 Tagen (Ende August) demonstrieren, dass 50% der Geburten innerhalb eines Zeitraums von etwa sechs Monaten stattfinden. Dies unterstreicht eine starke Konzentration früher Geburten, aber auch eine signifikante Verteilung über das gesamte Jahr.
Das Minimum von 14 Tagen und das Maximum von 364 Tagen zeigen, dass Spieler in England über das ganze Jahr verteilt geboren werden, mit einer leichten Präferenz für die ersten Monate.
3.3.4 Individualanalyse Spanien
Detaillierte Ergebnisse für Spanien:
· Minimum: 11 Tage
· Unteres Quartil: 98.25 Tage
· Median: 174 Tage
· Oberes Quartil: 208.25 Tage
· Maximum: 329 Tage
· Mittelwert: 168.69 Tage
· Standardabweichung: 92.79 Tage
· Differenz zwischen Mittelwert und Median: -5.31 Tage
Analyse
1. Verteilung der Geburtsdaten:
Der Median von 174 Tagen, der in etwa Mitte Juni entspricht, deutet darauf hin, dass die Hälfte der spanischen Spieler in der ersten Hälfte des Jahres geboren wird. Diese Platzierung des Medians weist auf eine moderate Präsenz des Relative Age Effects (RAE) hin, der ältere Spieler innerhalb ihres Jahrgangs bevorzugt.
Der Mittelwert von 168.69 Tagen, nahe am Median, deutet auf eine relativ symmetrische Verteilung der Geburtsmonate hin, was ungewöhnlich ist für Länder mit einem starken RAE. Die geringe negative Differenz zwischen Mittelwert und Median (-5.31 Tage) unterstützt dies und zeigt, dass eine signifikante Anzahl von Spielern auch später im Jahr geboren wird.
2. Quartile und Extremwerte:
Das untere Quartil bei 98.25 Tagen (Anfang April) und das obere Quartil bei 208.25 Tagen (Ende Juli) zeigen, dass 50% der Geburten innerhalb eines relativ engen Zeitraums von vier Monaten stattfinden. Dies könnte auf eine gewisse Konzentration der Geburten in diesen Monaten hindeuten.
Das Minimum von 11 Tagen und das Maximum von 329 Tagen belegen, dass die Geburten über das gesamte Jahr verteilt sind, was auf eine flexible und potenziell gerechtere Auswahl hinweisen könnte.
3.3.5 Individualanalyse Frankreich
Detaillierte Ergebnisse für Frankreich:
· Minimum: 10 Tage
· Unteres Quartil: 88 Tage
· Median: 159 Tage
· Oberes Quartil: 273 Tage
· Maximum: 354 Tage
· Mittelwert: 176.16 Tage
· Standardabweichung: 106.09 Tage
· Differenz zwischen Mittelwert und Median: 17.16 Tage
Analyse
1. Verteilung der Geburtsdaten:
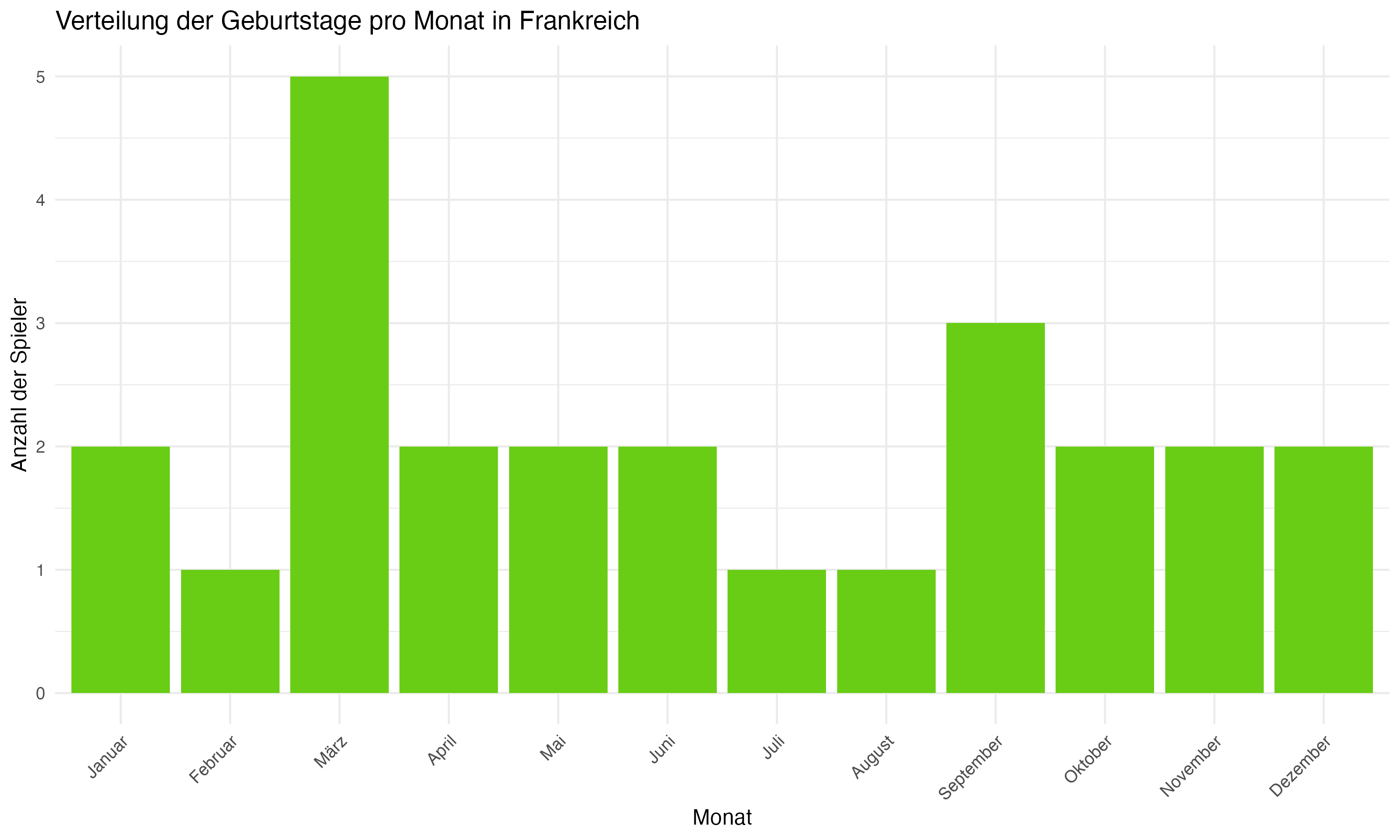
Der Median von 159 Tagen, der ungefähr Mitte Juni entspricht, zeigt, dass mehr als die Hälfte der französischen Spieler in der ersten Jahreshälfte geboren wird. Dies könnte auf eine moderate Ausprägung des Relative Age Effects (RAE) hindeuten, der ältere Spieler innerhalb ihres Jahrgangs bevorzugt.
Der Mittelwert liegt bei 176.16 Tagen, etwas später im Jahr als der Median, was auf eine rechtsschiefe Verteilung hindeutet. Dies bedeutet, dass eine bedeutende Anzahl von Spielern auch später im Jahr geboren wird, was die Annahme eines moderaten RAE unterstützt.
2. Quartile und Extremwerte:
Das untere Quartil bei 88 Tagen (Ende März) und das obere Quartil bei 273 Tagen (Ende September) zeigen, dass 50% der Geburten innerhalb eines breiteren Zeitraums von sechs Monaten stattfinden, was eine relativ gleichmäßige Verteilung der Geburtsmonate über das Jahr andeutet.
Das Minimum von 10 Tagen und das Maximum von 354 Tagen zeigen, dass Geburten fast das gesamte Jahr über stattfinden, was auf eine sehr heterogene Altersstruktur innerhalb der Spielerpopulation hindeutet.
3.3.6 Individualanalyse Portugal
Detaillierte Ergebnisse für Portugal:
· Minimum: 17 Tage
· Unteres Quartil: 73.25 Tage
· Median: 180.50 Tage
· Oberes Quartil: 259.50 Tage
· Maximum: 348 Tage
· Mittelwert: 182.65 Tage
· Standardabweichung: 105.27 Tage
· Differenz zwischen Mittelwert und Median: 2.15 Tage
Analyse
1. Verteilung der Geburtsdaten:
Der Median von 180.50 Tagen, der etwa Mitte Juni entspricht, zeigt, dass mehr als die Hälfte der portugiesischen Spieler in der ersten Jahreshälfte geboren wird. Diese Platzierung des Medians in der Mitte des Jahres könnte auf eine relativ ausgeglichene Verteilung der Geburtsmonate hinweisen, mit einer geringfügigen Tendenz zu älteren Spielern innerhalb ihres Jahrgangs.
Der Mittelwert von 182.65 Tagen, sehr nah am Median, unterstreicht eine sehr symmetrische Verteilung der Geburtsmonate. Die minimale Differenz zwischen Mittelwert und Median (2.15 Tage) weist darauf hin, dass es keine signifikante Schieflage in der Verteilung gibt.
2. Quartile und Extremwerte:
Das untere Quartil bei 73.25 Tagen (Anfang März) und das obere Quartil bei 259.50 Tagen (Anfang September) demonstrieren, dass 50% der Geburten innerhalb eines halben Jahres stattfinden. Dies zeigt eine breite Streuung der Geburtsdaten über das Jahr.
Das Minimum von 17 Tagen und das Maximum von 348 Tagen belegen, dass die Geburten über das gesamte Jahr verteilt sind, was auf eine heterogene Altersstruktur innerhalb der Spielerpopulation hindeutet.
3.3.7 Individualanalyse Niederlande
Detaillierte Ergebnisse für die Niederlande:
· Minimum: 12 Tage
· Unteres Quartil: 53.75 Tage
· Median: 131.50 Tage
· Oberes Quartil: 217.50 Tage
· Maximum: 345 Tage
· Mittelwert: 145.62 Tage
· Standardabweichung: 101.26 Tage
· Differenz zwischen Mittelwert und Median: 14.12 Tage
Analyse
1. Verteilung der Geburtsdaten:
Der Median von 131.50 Tagen, der etwa Anfang Mai entspricht, zeigt, dass die Mehrheit der niederländischen Spieler in der ersten Jahreshälfte geboren wird. Dies deutet auf eine Präsenz des Relative Age Effects (RAE) hin, wobei ältere Spieler innerhalb ihres Jahrgangs bevorzugt werden könnten.
Der Mittelwert liegt bei 145.62 Tagen, Mitte Mai, was auf eine relativ gleichmäßige Verteilung der Geburtsmonate hinweist. Die positive Differenz zwischen Mittelwert und Median (14.12 Tage) zeigt eine leicht rechtsschiefe Verteilung, was bedeutet, dass eine signifikante Anzahl von Spielern auch später im Jahr geboren wird.
2. Quartile und Extremwerte:
Das untere Quartil bei 53.75 Tagen (Ende Februar) und das obere Quartil bei 217.50 Tagen (Ende Juli) zeigen, dass 50% der Geburten innerhalb eines Zeitraums von etwa fünf Monaten stattfinden. Dies unterstreicht eine starke Konzentration früher Geburten, aber auch eine signifikante Verteilung über das gesamte Jahr.
Das Minimum von 12 Tagen und das Maximum von 345 Tagen belegen, dass die Geburten über fast das ganze Jahr verteilt sind, was auf eine heterogene Altersstruktur innerhalb der Spielerpopulation hindeutet.
3.3.6 Individualanalyse Österreich
Detaillierte Ergebnisse für Österreich:
· Minimum: 2 Tage
· Unteres Quartil: 78.25 Tage
· Median: 140 Tage
· Oberes Quartil: 204 Tage
· Maximum: 354 Tage
· Mittelwert: 143.69 Tage
· Standardabweichung: 89.07 Tage
· Differenz zwischen Mittelwert und Median: 3.69 Tage
Analyse
1. Verteilung der Geburtsdaten:
Der Median von 140 Tagen, der etwa Mitte Mai entspricht, zeigt, dass die Mehrheit der österreichischen Spieler in der ersten Jahreshälfte geboren wird. Dies deutet auf eine Präsenz des Relative Age Effects (RAE) hin, bei dem älteren Spieler innerhalb ihres Jahrgangs bevorzugt werden könnten.
Der Mittelwert von 143.69 Tagen, ebenfalls ungefähr Mitte Mai, weist auf eine recht ausgeglichene Verteilung der Geburtsmonate hin. Die geringe positive Differenz zwischen Mittelwert und Median (3.69 Tage) unterstreicht eine leichte rechtsschiefe Verteilung, was bedeutet, dass einige Spieler auch später im Jahr geboren werden, obwohl die Mehrheit früher geboren wird.
2. Quartile und Extremwerte:
Das untere Quartil bei 78.25 Tagen (Ende März) und das obere Quartil bei 204 Tagen (Ende Juli) zeigen, dass 50% der Geburten innerhalb eines relativ engen Zeitfensters von vier Monaten stattfinden. Dies deutet auf eine Konzentration der Geburten im Frühjahr bis frühen Sommer hin.
Das Minimum von nur 2 Tagen und das Maximum von 354 Tagen belegen, dass Geburten fast das gesamte Jahr über stattfinden, was eine heterogene Altersstruktur innerhalb der Spielerpopulation anzeigt.
4 Diskussion
Analyse und Interpretation der Forschungsergebnisse zum RAE
4.1 Diskussion zur Forschungsfrage 1
4.1.1 Häufigkeitsverteilung aller Spieler
Die Analyse der Geburtsmonatsverteilung beleuchtet potenzielle Einflüsse auf die Auswahl und Entwicklung junger Talente in Fußballakademien. Insbesondere die Monate Februar und Mai, in denen eine erhöhte Anzahl von Geburten festgestellt wurde, deuten darauf hin, dass Spieler, die in diesen Monaten geboren wurden, möglicherweise aufgrund physischer Reife und Altersvorteilen bevorzugt selektiert werden. Diese Erkenntnisse legen nahe, dass Trainer und Akademien ihre Auswahlkriterien überdenken sollten, um eine gleichmäßigere und gerechtere Talentförderung zu gewährleisten, die nicht vom Geburtsmonat abhängt.
4.1.2 Häufigkeitsverteilung nach Ländern
Die Unterschiede in der Geburtsmonatsverteilung zwischen verschiedenen europäischen Ländern werfen ein Schlaglicht auf die unterschiedlichen Ausprägungen des Relative Age Effects (RAE) und dessen Einfluss auf die Talententwicklung im Jugendfußball. In Ländern wie Deutschland, England und Spanien zeigt sich eine deutliche Konzentration von Geburtstagen in den ersten Monaten des Jahres. Dies könnte darauf hinweisen, dass in diesen Ländern der RAE besonders ausgeprägt ist und Spieler, die früher im Jahr geboren wurden, aufgrund von physischer Reife und damit verbundenen Leistungsvorteilen bevorzugt werden. Diese Tendenz könnte zu einer ungleichen Talentförderung führen und betont die Notwendigkeit einer kritischen Überprüfung und möglichen Anpassung der Auswahlprozesse in Fußballakademien.
Vergleichende Betrachtung: Länder wie die Slowakei und Ungarn eine zeigen eine gleichmäßigere Verteilung der Geburtsmonate, was auf weniger ausgeprägte RAE-Effekte oder unterschiedliche Auswahlkriterien in diesen Fußballsystemen hinweisen könnte. Diese Beobachtung ist von besonderem Interesse, da sie potenzielle kulturelle und systemische Unterschiede in der Talententwicklung aufzeigt. Es ist möglich, dass diese Länder effektivere Strategien implementiert haben, um den Einfluss des Geburtsmonats auf die Talentauswahl zu minimieren, oder dass sie andere Faktoren wie technische Fähigkeiten und Spielfähigkeit stärker gewichten.
4.2 Diskussion zur Forschungsfrage 2
Die zweite Forschungsfrage konzentrierte sich auf die Verteilung der Geburtstage in Tageszahlen und bot eine detailliertere Analyse der Altersstruktur und potenzielle Auswirkungen des Relative Age Effects (RAE) bei den Teilnehmern der Europameisterschaft. Die statistische Aufarbeitung der Geburtstage in Tagesform hat eine nuanciertere Betrachtung der Daten ermöglicht, die über die herkömmliche monatsbasierte Analyse hinausgeht.
Tiefere Einblicke durch Tag-genauere Daten: Die Umwandlung von Geburtsmonaten in genaue Tage des Jahres (von 1 bis 365) hat eine präzisere Analyse der Altersverteilung innerhalb des Teilnehmerfeldes ermöglicht. Diese Methode hat gezeigt, dass die Geburtstage sich über das gesamte Kalenderjahr erstrecken, mit signifikanten Spitzen und Tiefen, die Rückschlüsse auf die Selektionspraxis und Talententwicklung zulassen.
Statistische Maßzahlen und ihre Implikationen: Die spezifischen Maßzahlen wie Minimum, Quartile, Median, Mittelwert und Maximum haben aufgedeckt, dass die meisten Geburtstage innerhalb der ersten drei Quartale des Jahres konzentriert sind, was auf eine mögliche Bevorzugung von Spielern hinweist, die früher im Jahr geboren wurden. Der Median lag etwa Mitte Mai, während der Durchschnittswert etwas später im Jahr, ungefähr Mitte Juni, lag. Diese leichte Rechtsschiefe in der Verteilung kann darauf hindeuten, dass Spieler, die in der ersten Jahreshälfte geboren wurden, tendenziell älter und somit bei der Auswahl für Jugendprogramme möglicherweise bevorzugt werden.
Diskussion über den Einfluss des RAE: Die Erkenntnisse unterstützen die Theorie, dass der RAE in der frühkindlichen Entwicklung und Selektion von Fußballspielern eine Rolle spielt. Spieler, die früher im Jahr geboren wurden, könnten aufgrund zusätzlicher Reife und physischer Entwicklung bevorzugt werden. Diese Tendenz kann langfristige Auswirkungen auf die Karrierechancen der Spieler haben und führt zu einer ungleichen Verteilung der Chancen, die auf dem Geburtsmonat basieren.
4.3 Diskussion der Fragen 1 und 2: Implikationen und Empfehlungen für die Talentförderung
Die erkennbaren Muster und Unterschiede in der Geburtsmonatsverteilung der Spieler aus verschiedenen Ländern sowie die detaillierte Tagesanalyse der Geburtstage liefern wertvolle Einsichten in die Auswirkungen des Relative Age Effects (RAE). Diese Ergebnisse sollten als Anregung für Trainer, Akademieleiter und sportpolitische Entscheidungsträger dienen, bestehende Auswahl- und Trainingsmethoden zu überdenken. Die Implementierung von altersrelativen Klassen oder die Anpassung von Trainings- und Bewertungsmethoden könnten dazu beitragen, die durch den RAE verursachten Ungleichheiten zu reduzieren und eine gerechtere Talentförderung zu fördern. Zusätzlich könnten altersunabhängige Bewertungskriterien oder die Einrichtung von Entwicklungsprogrammen, die alle Spieler unabhängig von ihrem Geburtsmonat gleich behandeln, eingeführt werden, um eine gleichmäßigere Chancenverteilung zu gewährleisten.
Weitere Forschungen sind notwendig, um die langfristigen Auswirkungen des RAE auf die Karriereentwicklung von Spielern zu verstehen und effektive Strategien zu entwickeln, die dessen negative Auswirkungen abmildern können. Es wäre sinnvoll, die Forschung auf Länder auszudehnen, die bisher nicht im Fokus standen, und vergleichende Studien zwischen verschiedenen Sportarten und Kulturen durchzuführen, um globale Muster und Unterschiede im Umgang mit dem RAE zu identifizieren. Solche Studien könnten tiefere Einsichten in die Mechanismen hinter dem RAE bieten und dazu beitragen, umfassendere Dokumentationen seiner Auswirkungen zu erstellen.
Abschließend unterstreichen die Ergebnisse die Bedeutung einer gerechten Talentförderung und bieten eine solide Grundlage für die Anpassung von Trainings- und Auswahlmethoden im professionellen Jugendfußball. Durch gezielte Maßnahmen gegen den RAE können gerechtere und effektivere Entwicklungsprogramme etabliert werden, die allen Spielern, unabhängig von ihrem Geburtsdatum, gleiche Chancen bieten.
4.4 Diskussion zur Forschungsfrage 3
Die dritte Forschungsfrage dieser Studie zielt darauf ab, die spezifischen Unterschiede in der Geburtsdatenverteilung der Fußballspieler aus verschiedenen Ländern zu analysieren, die es bis ins Achtelfinale der Europameisterschaft geschafft haben. Diese detaillierten Analysen erlauben es, die Auswirkungen des Relative Age Effects (RAE) auf individueller Länderebene zu diskutieren und tiefergehende Einblicke in die Selektionsmechanismen und Entwicklungsstrategien der jeweiligen Fußballakademien zu gewinnen.
4.4.1 Diskussion Schweiz
Die Ergebnisse für die Schweiz zeigen eine ungewöhnliche Verteilung, bei der der Median und Mittelwert später im Jahr liegen als in den meisten anderen europäischen Ländern. Dies könnte darauf hindeuten, dass der RAE in der Schweiz weniger ausgeprägt ist oder dass andere Faktoren wie technische Fähigkeiten oder psychosoziale Aspekte eine größere Rolle in der Talentförderung spielen. Möglicherweise verfolgt die Schweiz effektivere Methoden, die den Geburtsmonat als Selektionskriterium minimieren, was zu einer faireren Talententwicklung führt. Link zum Schweizer Fußballverband.
4.4.2 Diskussion Deutschland
In Deutschland zeigt sich eine starke Tendenz, dass Spieler, die in den ersten Monaten des Jahres geboren wurden, bevorzugt werden, was typisch für den Einfluss des RAE ist. Diese Praxis könnte langfristig die Chancen für Spieler, die später im Jahr geboren wurden, einschränken. Es wird empfohlen, dass deutsche Fußballakademien ihre Auswahlkriterien überdenken, um eine gleichmäßigere Chancenverteilung zu gewährleisten und eventuell altersunabhängige Bewertungsverfahren zu implementieren. Link zum Deutschen Fußballverband(DFB).
4.4.3 Diskussion England
Auch die englischen Daten bestätigen die Existenz des RAE. Die Erkenntnis, dass Spieler, die früher im Jahr geboren wurden, tendenziell bevorzugt werden, sollte die Fußballakademien in England veranlassen, ihre Trainings- und Selektionsstrategien zu überdenken. Ziel sollte es sein, faire Bedingungen zu schaffen, die allen Spielern unabhängig von ihrem Geburtsmonat gleiche Entwicklungs- und Aufstiegschancen bieten. Link zum Englischen Fußballverband (FA).
4.4.4 Diskussion Spanien
Die Analyse der spanischen Spielerdaten lässt eine moderate Auswirkung des RAE erkennen. Die vergleichsweise gleichmäßige Verteilung der Geburtsmonate könnte ein Indikator dafür sein, dass in Spanien eine breitere Palette an Talenten berücksichtigt wird und die Talentauswahl weniger von physischen Reifevorteilen beeinflusst wird. Dies ist ein positives Zeichen für eine gerechte Talentförderung. Link zum Spanischen Fußballverband.
4.4.5 Diskussion Frankreich
Die Daten aus Frankreich weisen darauf hin, dass der RAE vorhanden, aber möglicherweise nicht so stark ausgeprägt ist wie in anderen Ländern. Die breite Streuung der Geburtsmonate könnte bedeuten, dass die Talentauswahl in Frankreich vielfältiger ist und weniger von Altersvorteilen abhängig gemacht wird. Dies könnte zu einer gerechteren Entwicklung aller Talente führen. Link zum Französischen Fußballverband.
4.4.6 Diskussion Portugal
Portugal zeigt eine der ausgewogensten Geburtsdatenverteilungen, was darauf hinweist, dass der RAE dort möglicherweise eine geringere Rolle spielt. Diese gerechtere Verteilung könnte dazu beitragen, dass Spieler unabhängig von ihrem Geburtsmonat gleiche Chancen auf Entwicklung und Auswahl erhalten. Link zum Portugiesischen Fußballverband.
4.4.7 Diskussion Niederlande
Die Niederlande zeigen ähnliche Tendenzen wie Deutschland und England, was den RAE betrifft. Auch hier könnte eine Überarbeitung der Selektionsstrategien angebracht sein, um sicherzustellen, dass Talente fair und unabhängig von ihrem Geburtsdatum gefördert werden. Link zum Niederländischen Fußballverband.
4.4.8 Diskussion Österreich
Die österreichischen Daten bestätigen ebenfalls eine gewisse Präsenz des RAE, allerdings mit einer relativ gleichmäßigen Verteilung der Geburtsmonate im Frühjahr bis Sommer. Dies könnte darauf hindeuten, dass ältere Spieler innerhalb ihres Jahrgangs bevorzugt werden, was eine Anpassung der Auswahlmethoden erfordern könnte. Link zum Österreichischen Fußballverband.
Diese individuellen Analysen verdeutlichen, wie unterschiedlich der RAE in verschiedenen europäischen Ländern wirken kann und unterstreichen die Notwendigkeit für Fußballakademien, ihre Methoden kontinuierlich zu hinterfragen und anzupassen, um eine gerechtere und effektivere Talentförderung zu gewährleisten.
5 Schlussfolgerungen
Diese Studie hat umfassend die Auswirkungen des Relative Age Effects (RAE) auf die Teilnehmer der Europameisterschaft 2024 untersucht. Unsere Analysen der Geburtsmonatsverteilungen unterstreichen, wie tiefgreifend das Geburtsdatum die Chancen junger Fußballspieler beeinflusst, ausgewählt und gefördert zu werden. Insbesondere zeigt sich, dass Spieler, die in den ersten Monaten des Jahres geboren wurden, systematische Vorteile genießen, was auf die Prävalenz des RAE in vielen europäischen Fußballakademien hinweist.
Die länderspezifischen Analysen bieten wertvolle Einsichten in die unterschiedlichen Ausprägungen und Umgangsweisen mit dem RAE. Während einige Länder wie Deutschland, England und Spanien starke Tendenzen aufzeigen, die frühe Geburtsmonate bevorzugen, demonstrieren andere, wie die Schweiz und Portugal, eine gerechtere Verteilung, was auf effektivere Ansätze in der Talentselektion hindeuten könnte.
Die Ergebnisse legen nahe, dass eine Überprüfung und mögliche Anpassung der Auswahl- und Trainingsmethoden in Fußballakademien erforderlich sind, um eine gerechtere Talentförderung zu gewährleisten. Dies könnte durch die Implementierung von altersunabhängigen Bewertungskriterien oder durch die Einrichtung von Entwicklungsprogrammen geschehen, die alle Spieler unabhängig von ihrem Geburtsmonat gleich behandeln.
Abschließend zeigt diese Studie die Notwendigkeit auf, weiterhin den Einfluss des Geburtsmonats auf die Talentauswahl und -förderung intensiv zu erforschen. Durch gezielte Maßnahmen gegen den RAE können gerechtere und effektivere Entwicklungsprogramme im Jugendfußball etabliert werden, die allen Spielern, unabhängig von ihrem Geburtsdatum, gleiche Chancen bieten. Zukünftige Forschungen sollten sich darauf konzentrieren, die langfristigen Auswirkungen des RAE auf die Karriereentwicklung von Spielern zu untersuchen und effektive Strategien zu entwickeln, um dessen negative Auswirkungen zu mindern.
Literatur
Doncaster, G., Kelly, A. L., McAuley, A. B. T., Cain, A., Partington, M., Nelson, L. & O’Gorman, J. (2024). Relative Age Effects and the Premier League’s Elite Player Performance Plan (EPPP): A Comparison of Birthdate Distributions Within and Between Age Groups. Journal Of Science in Sport And Exercise. https://doi.org/10.1007/s42978-024-00285-w
Lames, M., PhD, Augste, C., Dreckmann, C., Görsdorf, K. & Schimanski, M. (o. D.). Der „Relative Age Effect“ (RAE): neue Hausaufgaben für den Sport. In TRAININGSLEHRE LEISTUNGSSPORT (Bd. 6, Nummer 20084, S. Eingegangen). https://opus.bibliothek.uni-augsburg.de/opus4/frontdoor/deliver/index/docId/76156/file/lsp08_06_4_9.pdf
Romann, M., Javet, M. & Fuchslocher, J. (2015). Relative Age Effect im Kinder-und Juniorenfussball. Unbekannt. https://doi.org/10.13140/rg.2.1.2024.2403
Saavedra-García, M. A., Santiago-Alonso, M., Vila-Suárez, H., Montero-Seoane, A. & Fernández-Romero, J. J. (2024). Relative Age Effect Analysis in the History of the Ballon d’Or (1956–2023). Sports, 12(4), 115. https://doi.org/10.3390/sports12040115
Schröpf, B. (2018). Relative Age Effect und Karrieremuster im deutschen Nachwuchsleistungsfußball. In M. Lames & A. Hohmann (Hrsg.), Fakultät für Sport- und Gesundheitswissenschaften [Thesis]. https://mediatum.ub.tum.de/doc/1454491/document.pdf
Anhang
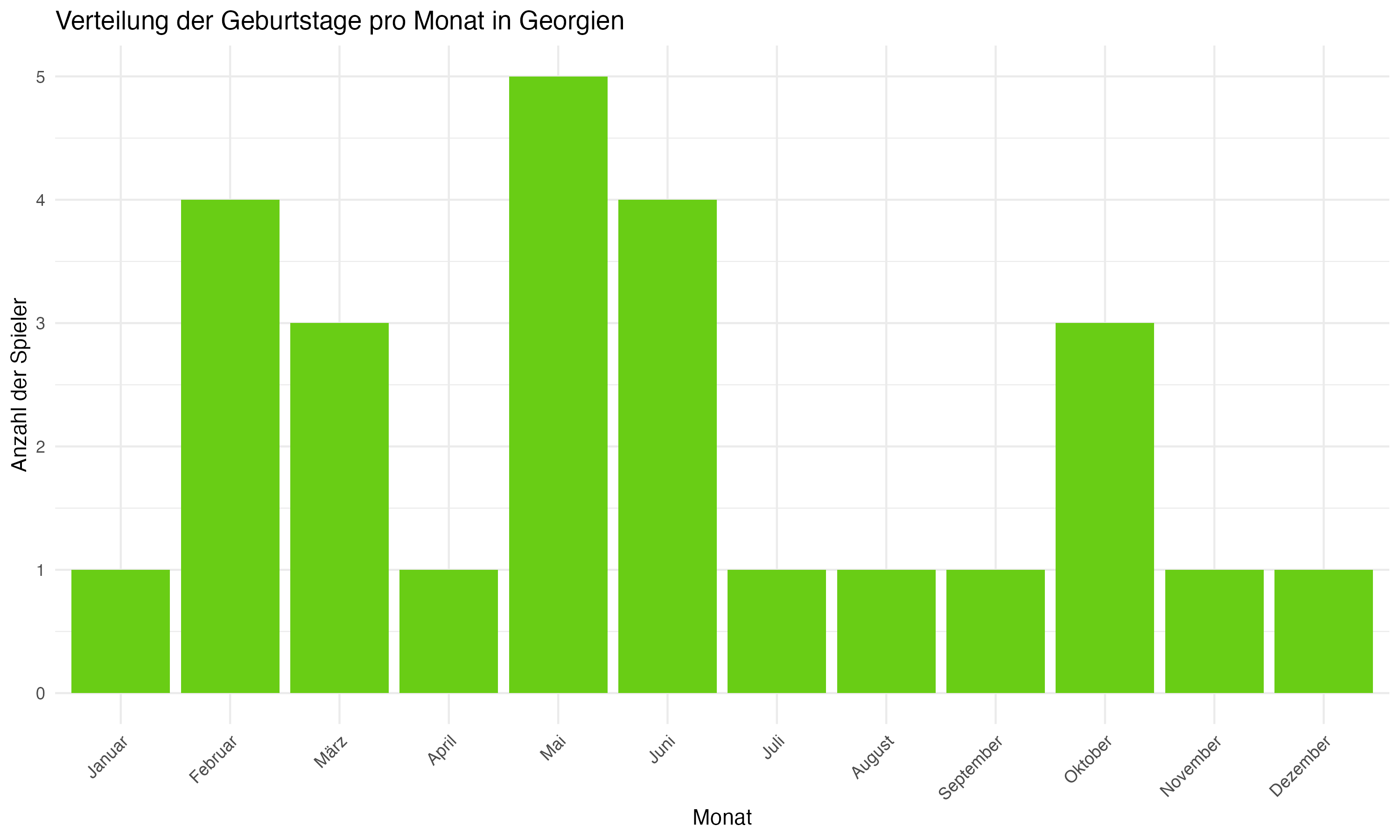
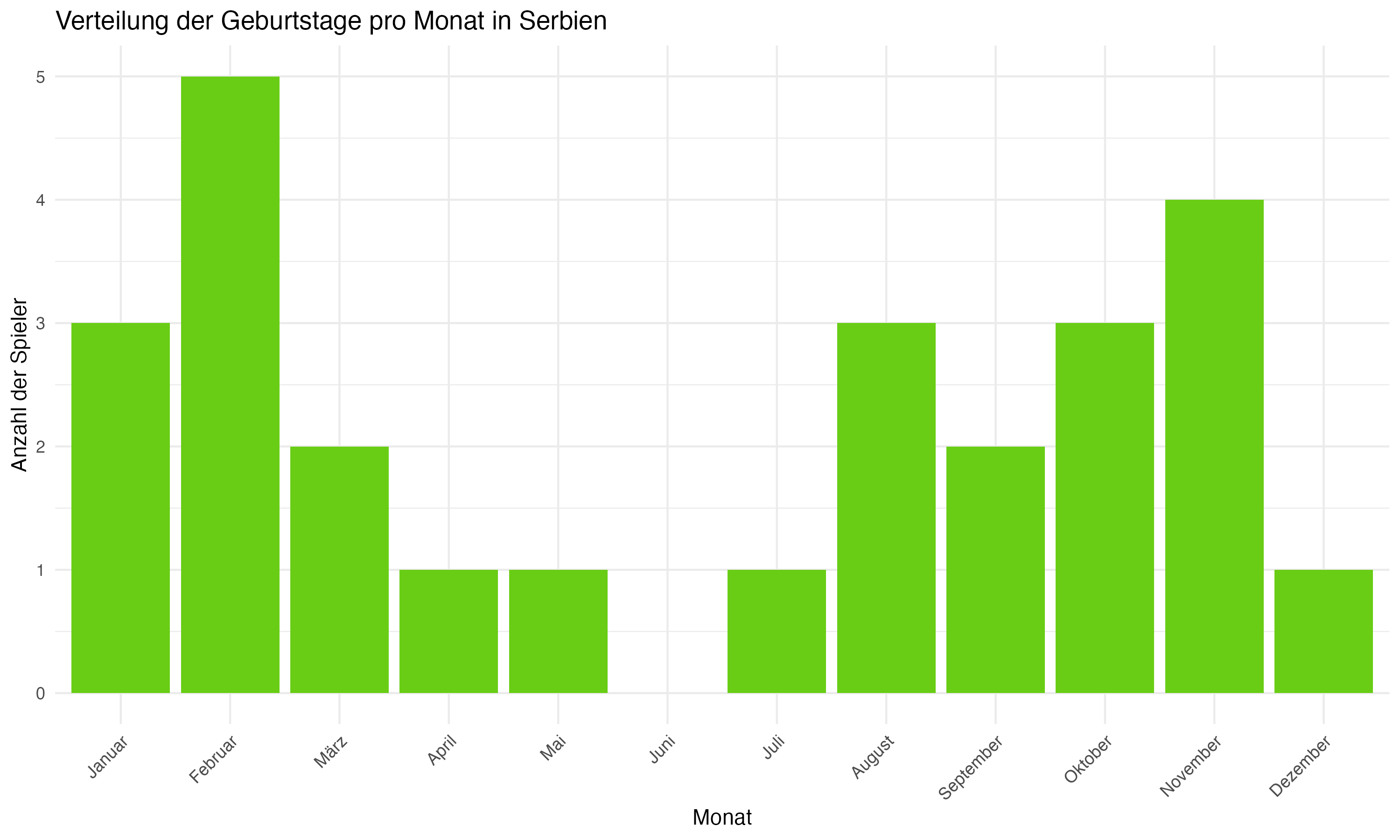
Anhang 1: Plots zur Forschungsfrage 1 (Monatsverteilungen)

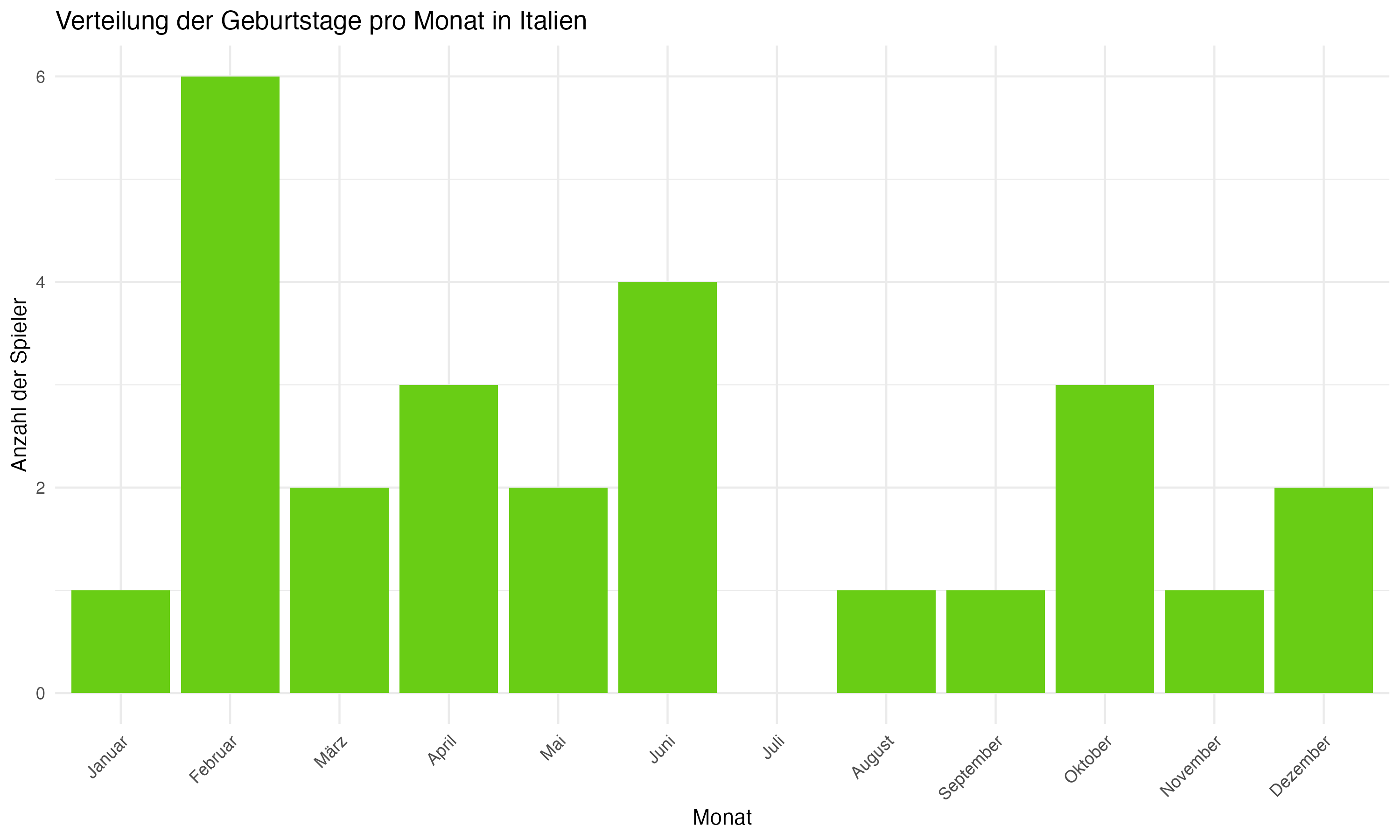
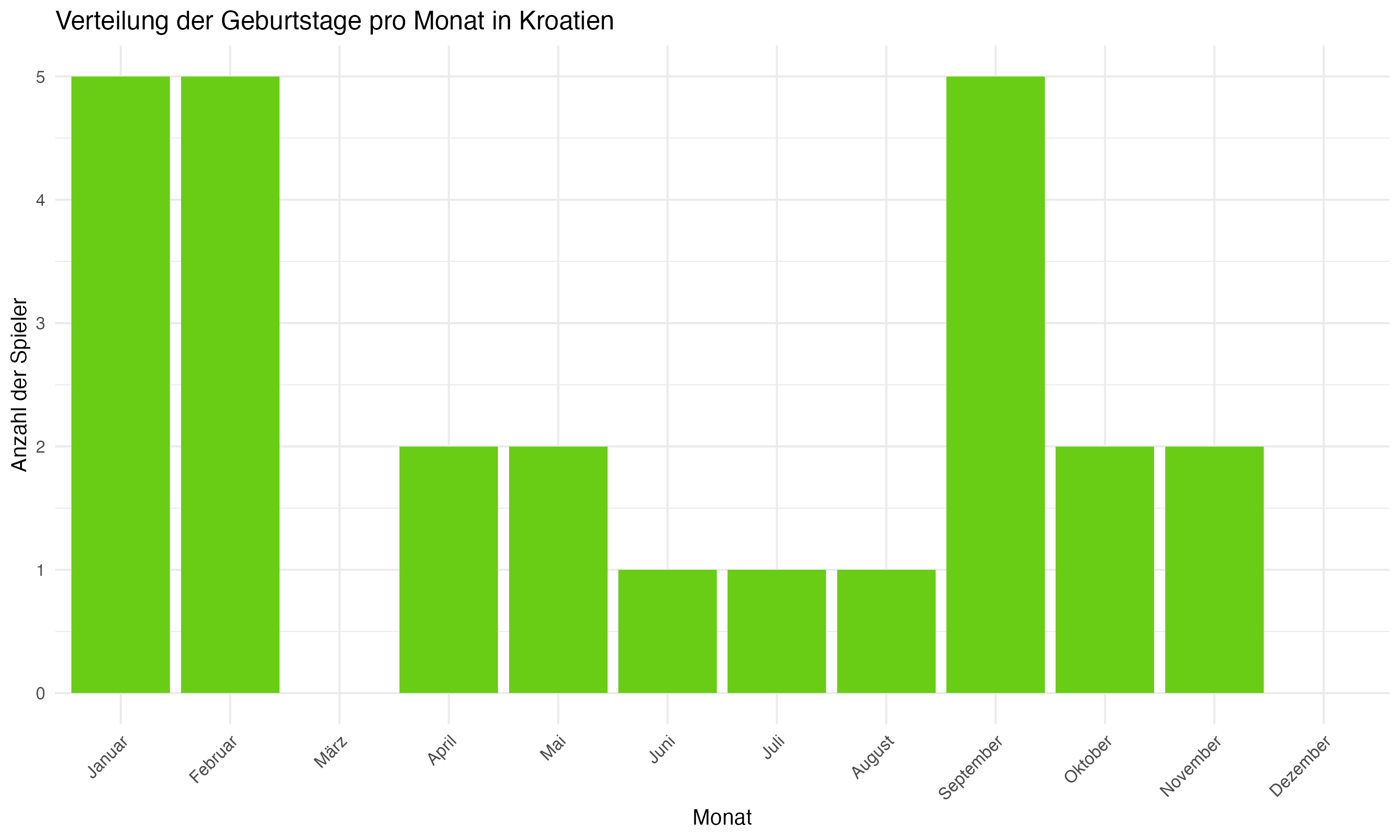
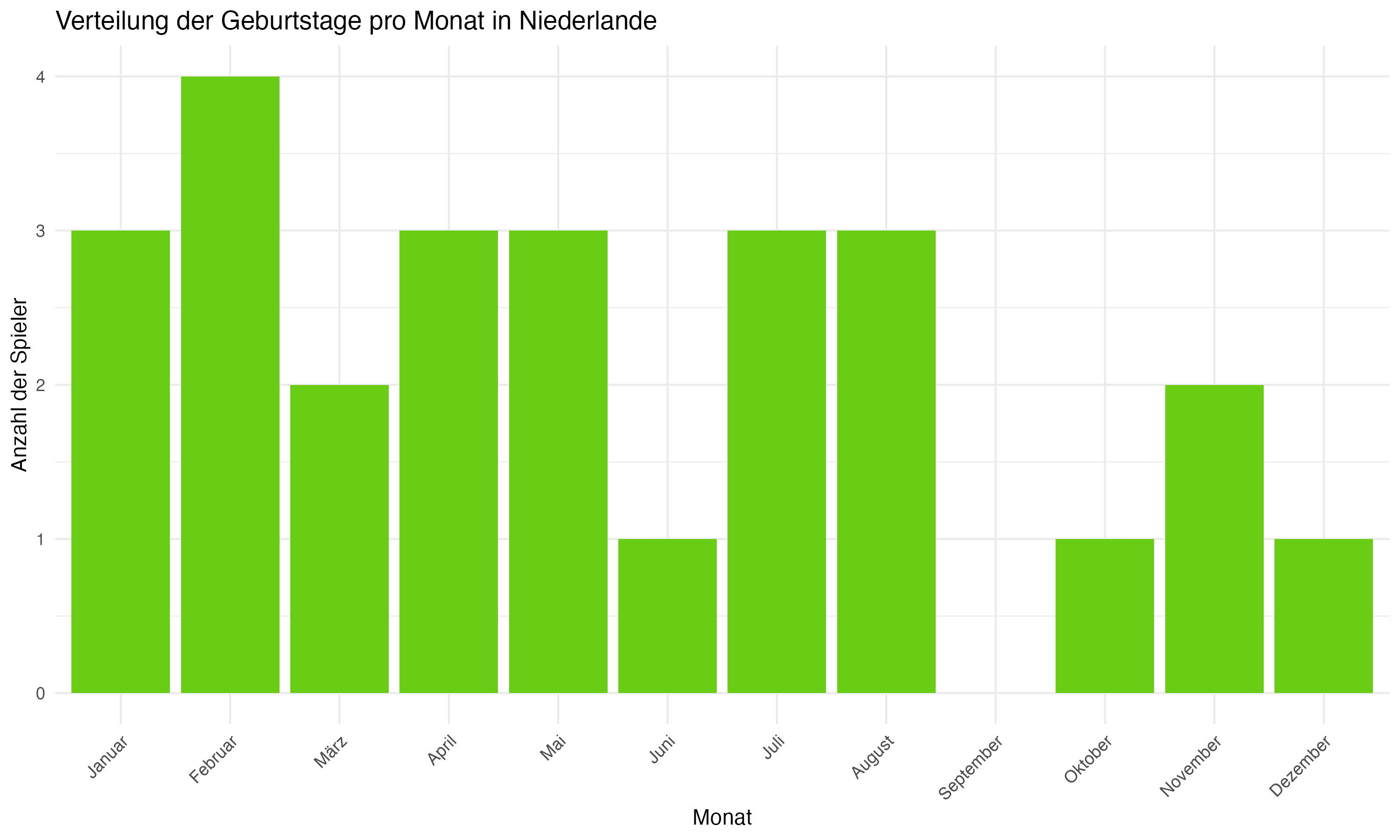
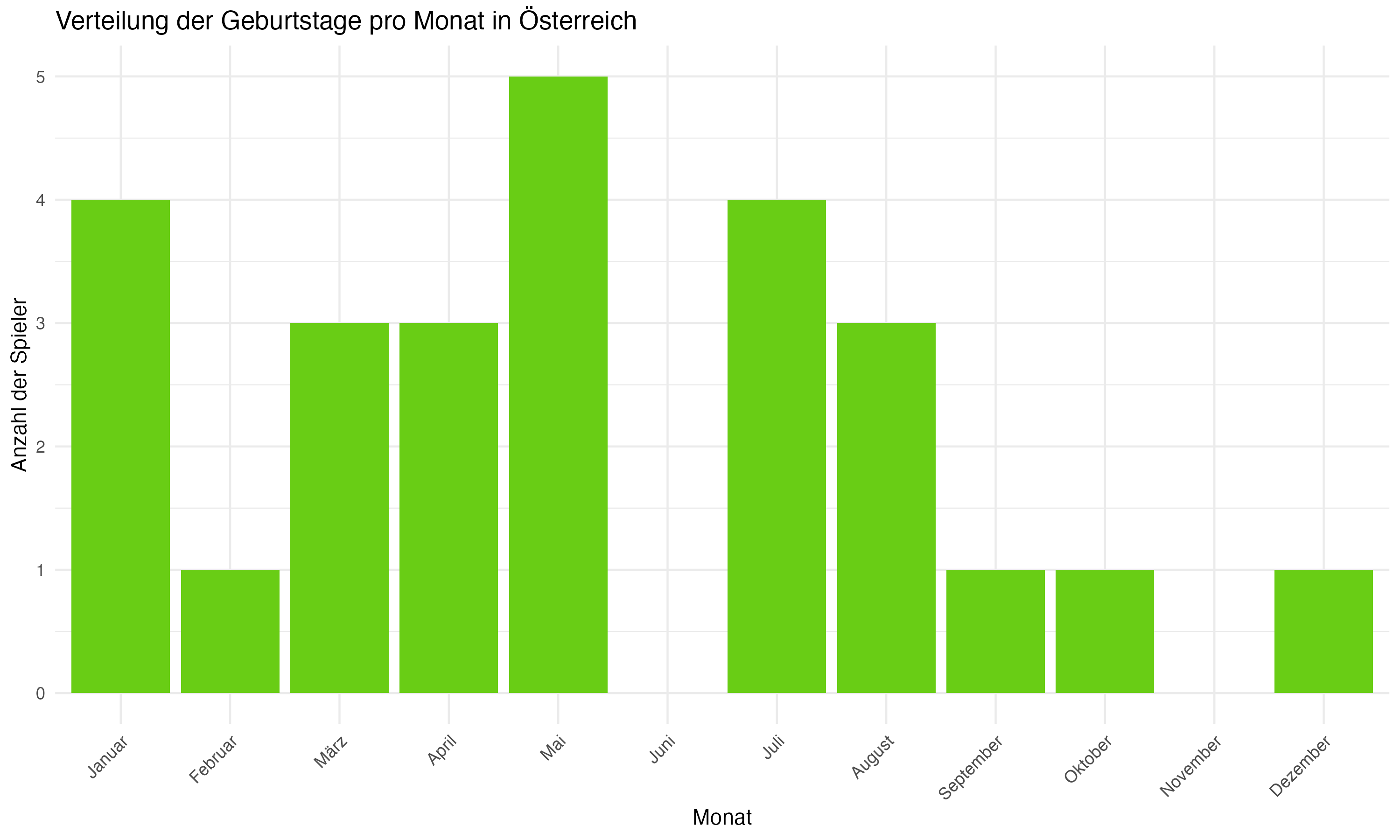
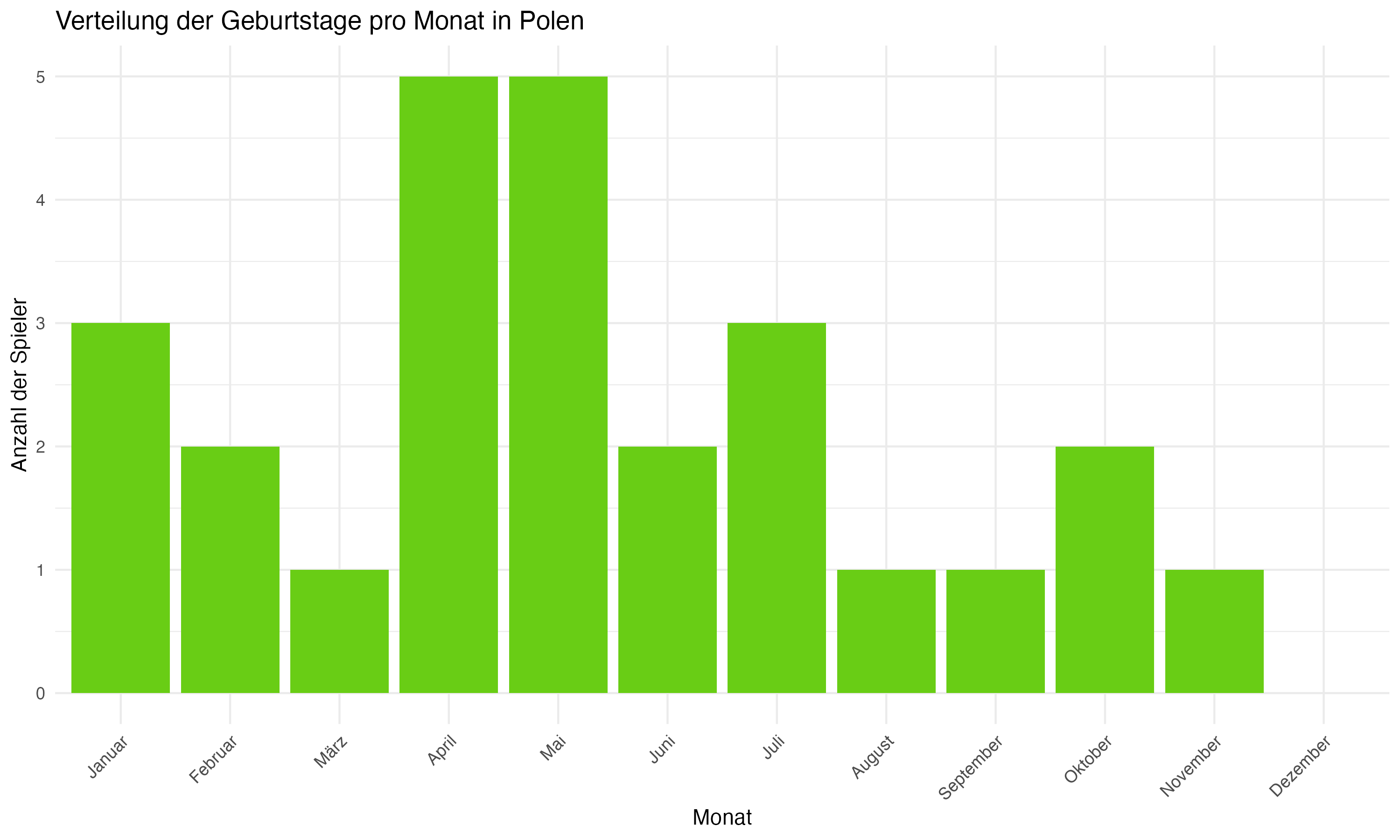
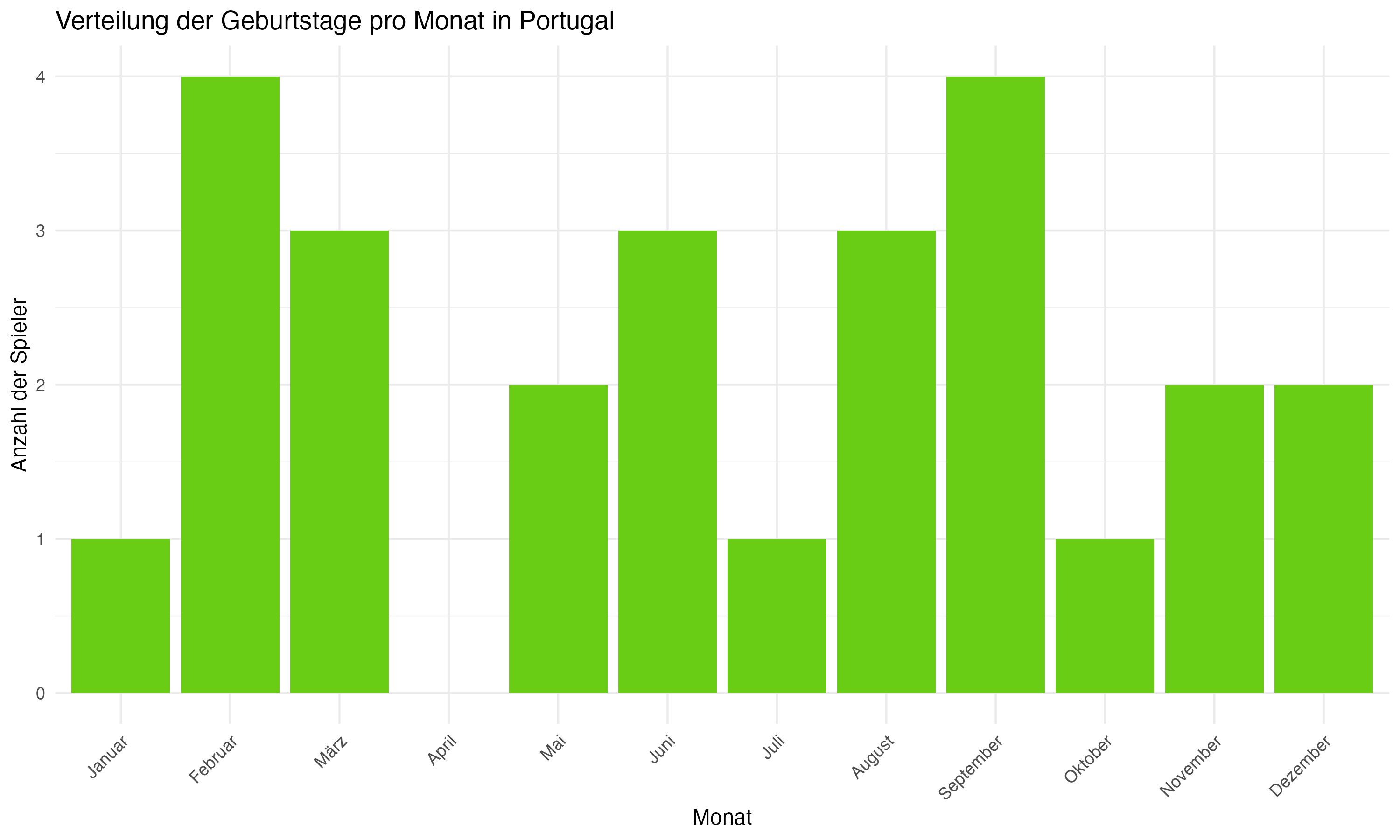
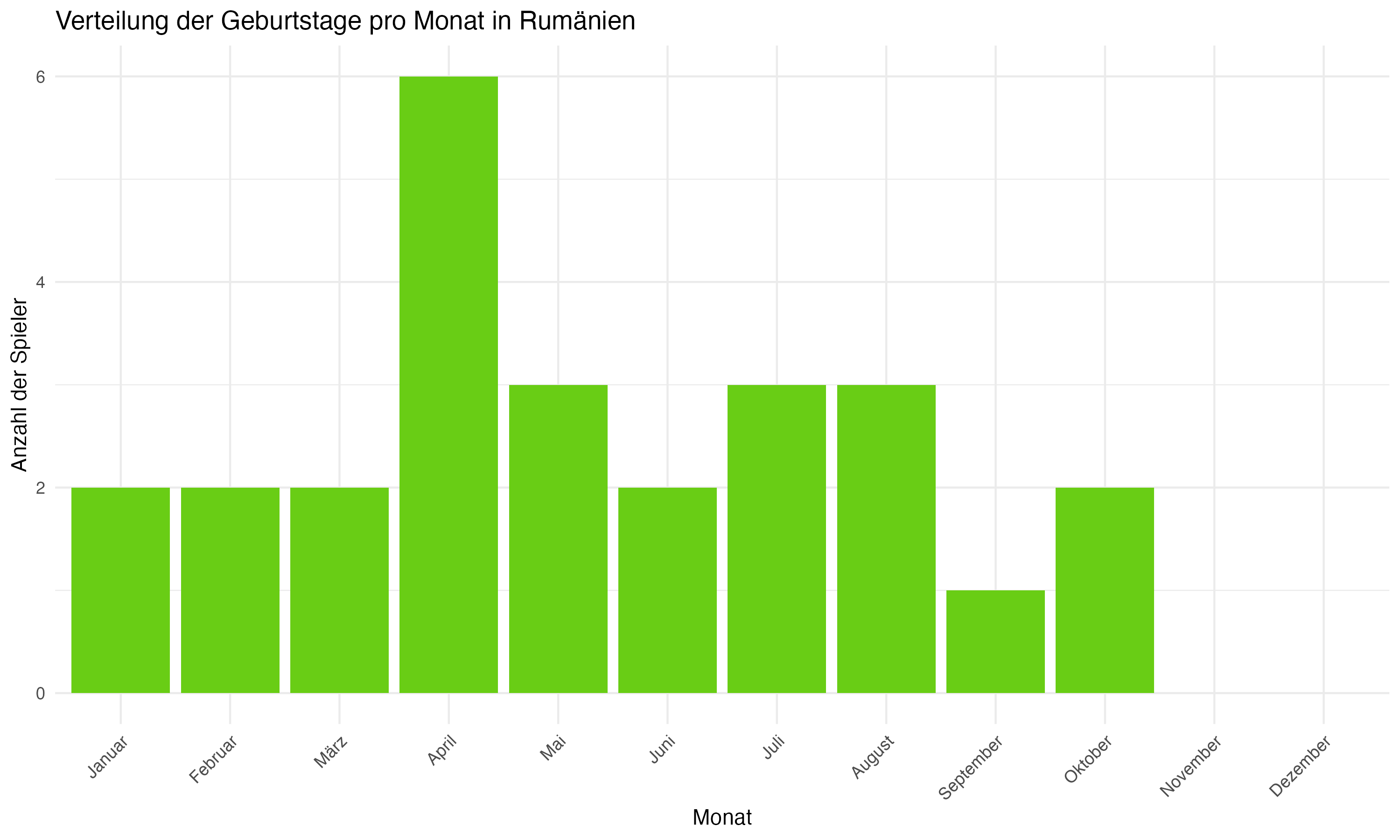
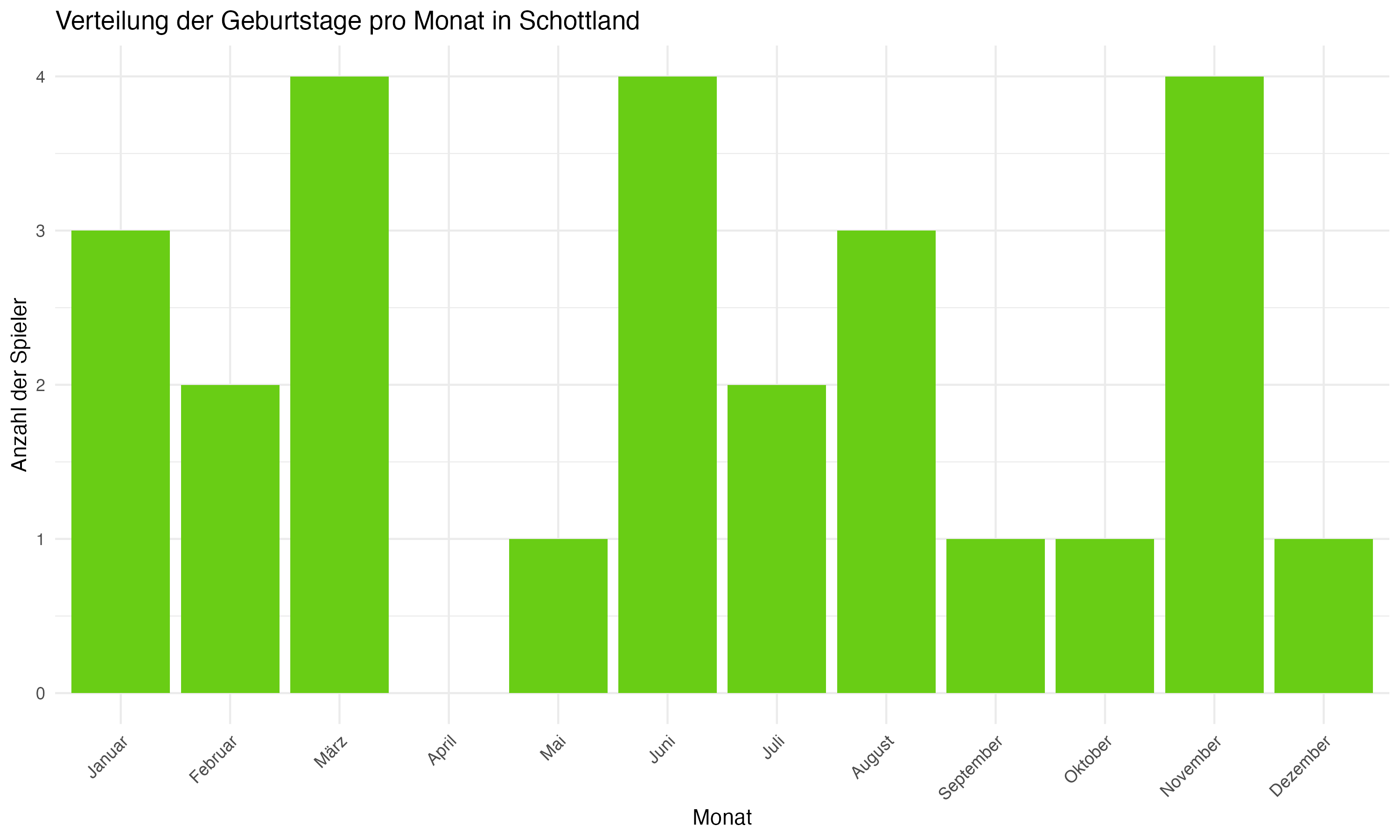
Anhang 2: R Code
Codeblock 1: Monatsberechnungen
# Installiere und lade erforderliche Pakete
library(lubridate)
library(ggplot2)
library(dplyr)
library(tidyr)
library(DT)
library(htmltools)
# Daten laden, aktiviere dataframe
# Altersverteilung_EM_Spieler_2
#1. Datenbereinigung
# Umwandeln in eine englische Schreibweise
Altersverteilung_EM_Spieler_2 <- Altersverteilung_EM_Spieler_2 %>%
mutate(GebDatA = as.Date(GebDat, format = "%d.%m.%Y"))
# Formatieren der Datumswerte für die Anzeige oder den Export
Altersverteilung_EM_Spieler_2 <- Altersverteilung_EM_Spieler_2 %>%
mutate(GebDatAFormatted = format(GebDatA, "%Y-%m-%d"))
# 2. Berechne die Verteilung der Geburtstage pro Monat und pro Land
birth_month_country_distribution <- Altersverteilung_EM_Spieler_2 %>%
mutate(Geburtsmonat = month(GebDatAFormatted)) %>% # Extrahiert den Monat aus dem Geburtsdatum
group_by(Land, Geburtsmonat) %>%
summarise(Anzahl = n()) # Zählt die Anzahl der Geburtstage pro Monat und Land
print(birth_month_country_distribution)
# 3. Umformen des DataFrames, um die Länder auf der Y-Achse und die Monate auf der X-Achse anzuzeigen
wide_birth_month_distribution <- birth_month_country_distribution %>%
mutate(Geburtsmonat = factor(Geburtsmonat, levels = 1:12, labels = c("Januar", "Februar", "März", "April", "Mai", "Juni", "Juli", "August", "September", "Oktober", "November", "Dezember"))) %>%
pivot_wider(names_from = Geburtsmonat, values_from = Anzahl, values_fill = list(Anzahl = 0))
# Explizite Anpassung der Spaltenreihenfolge nach der Umwandlung
wide_birth_month_distribution <- wide_birth_month_distribution %>%
select(Land, "Januar", "Februar", "März", "April", "Mai", "Juni", "Juli", "August", "September", "Oktober", "November", "Dezember")
# Anzeige der umgeformten Tabelle
print(wide_birth_month_distribution)
# 4. Tabellenexport als .html
# Erstellen der interaktiven Tabelle mit angepassten Optionen
interactive_table <- datatable(
wide_birth_month_distribution,
options = list(
pageLength = -1, # Alle Zeilen auf einer Seite anzeigen
autoWidth = TRUE, # Automatische Breitenanpassung der Spalten
dom = 'Bfrtip', # Konfiguration des Table-Layouts (Buttons, Suchfeld, Pagination)
buttons = c('copy', 'csv', 'excel', 'pdf', 'print'), # Ermöglichen des Exports und Druckens
order = list(list(1, 'asc')), # Standardmäßiges Sortieren nach der ersten Spalte (Land)
language = list(url = '//cdn.datatables.net/plug-ins/1.11.5/i18n/German.json') # Deutsche Spracheinstellungen
),
caption = htmltools::tags$caption(
style = "caption-side: top; text-align: center; font-size: 18px;",
'Verteilung der Geburtstage pro Monat und Land'
)
)
# Speichern der Tabelle als HTML-Datei ohne Footer
saveWidget(interactive_table, 'wide_birth_month_distribution.html', selfcontained = TRUE)
# 5. Erstelle ein Facettendiagramm
# Definiere eine benutzerdefinierte Farbpalette
custom_colors <- rep(c("green4", "orange"), length.out = length(unique(birth_month_country_distribution$Land)))
# Erstellen eines Facettendiagramms, um die Verteilung der Geburtstage pro Land und Monat zu zeigen
p <- ggplot(birth_month_country_distribution, aes(x = factor(Geburtsmonat, labels = month.abb), y = Anzahl, fill = Land, group = Land)) +
geom_bar(stat = "identity", position = "dodge", width = 0.7) +
geom_line(aes(y = Anzahl, group = 1), color = "grey80", size = 0.5) + # Hinzufügen einer Linie zur Verdeutlichung der Verteilung
geom_point(aes(y = Anzahl), color = "grey80", size = 1) + # Hinzufügen von Punkten zur Verdeutlichung der Verteilung
facet_wrap(~ Land, scales = "fixed") + # Sicherstellen, dass alle Facetten die gleiche y-Achse haben
scale_fill_manual(values = custom_colors) + # Verwendung der benutzerdefinierten Farbpalette
labs(title = "Verteilung der Geburtstage pro Monat und Land",
x = "Monat",
y = "Anzahl der Geburtstage") +
theme_minimal() +
theme(axis.text.x = element_text(angle = 45, hjust = 1), # Drehung der x-Achsen-Beschriftungen für bessere Lesbarkeit
plot.title = element_text(size = 16, face = "bold"), # Größerer Titel
axis.title = element_text(size = 14), # Größere Achsentitel
legend.position = "none", # Entfernung der Legende für eine übersichtlichere Darstellung
panel.grid.major = element_line(color = "grey80"), # Hinzufügen von Gitternetzlinien
panel.grid.minor = element_blank())
print(p)
# Speichern des Plots als PNG
ggsave("birthdays_distribution.png", plot = p, width = 10, height = 6, dpi = 300)
# 6. jetzt möchte ich noch für jedes Land einen Barplot erstellen
# Annahme, dass 'birth_month_country_distribution' die Spalte 'Geburtsmonat' hat, die numerisch ist
# Umwandeln des numerischen Monats in Monatsnamen ohne die Originalspalte 'Geburtsmonat' zu überschreiben
birth_month_country_distribution <- birth_month_country_distribution %>%
mutate(GeburtsmonatName = factor(Geburtsmonat, levels = 1:12, labels = c("Januar", "Februar", "März", "April", "Mai", "Juni", "Juli", "August", "September", "Oktober", "November", "Dezember")))
# Erstellen einer Tabelle mit allen Kombinationen von Ländern und Monatsnamen
all_combinations <- expand.grid(Land = unique(birth_month_country_distribution$Land),
GeburtsmonatName = levels(birth_month_country_distribution$GeburtsmonatName))
# Zusammenführen mit den vorhandenen Daten, um sicherzustellen, dass alle Monate vertreten sind
complete_data <- left_join(all_combinations, birth_month_country_distribution, by = c("Land", "GeburtsmonatName")) %>%
replace_na(list(Anzahl = 0)) # Ersetzen von NA mit 0
# Eindeutige Liste der Länder extrahieren
unique_countries <- unique(complete_data$Land)
# Schleife durch jedes Land und erstelle einen Plot
for (land in unique_countries) {
country_data <- filter(complete_data, Land == land)
file_name <- paste0("Barplot_", land, ".png") # Dateiname nur einmal definieren
# Erstellen des Barplots mit festgelegter Farbe außerhalb von aes()
p <- ggplot(country_data, aes(x = GeburtsmonatName, y = Anzahl)) +
geom_bar(stat = "identity", fill = "#69CD15") + # Feste Farbe hier setzen
labs(title = paste("Verteilung der Geburtstage pro Monat in", land),
x = "Monat",
y = "Anzahl der Spieler") +
theme_minimal() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))
ggsave(filename = file_name, plot = p, width = 10, height = 6, dpi = 300)
}
# 7. jetzt möchte ich ein Häufigkeitsdiagramm von allen Einträgen haben, unabhängig vom Land
# Daten aggregieren, um die Gesamtanzahl der Geburtstage pro Monat zu erhalten
total_births_per_month <- birth_month_country_distribution %>%
group_by(GeburtsmonatName) %>%
summarise(Total_Anzahl = sum(Anzahl)) %>%
ungroup()
# Durchschnitt der Gesamtanzahl der Geburtstage berechnen
average_births <- mean(total_births_per_month$Total_Anzahl)
# Erstellen des Barplots für die Gesamtanzahl der Geburtstage pro Monat
p <- ggplot(total_births_per_month, aes(x = GeburtsmonatName, y = Total_Anzahl)) +
geom_bar(stat = "identity", fill = "#69CD15") + # Setzen der Farbe auf green4
geom_hline(yintercept = average_births, linetype = "dashed", color = "red", size = 1.0) +
labs(title = "Gesamtverteilung der Geburtstage pro Monat",
x = "Monat",
y = "Gesamtanzahl der Geburtstage") +
theme_minimal() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))
# Anzeigen des Plots
print(p)
# Optional: Speichern des Plots als PNG
ggsave(filename = "Total_Birthdays_Per_Month.png", plot = p, width = 10, height = 6, dpi = 300)
print(total_births_per_month)
Codeblock 2: Tagesberechnungen
# Geburtsdaten in Tage umgerechnet
library(dplyr)
library(lubridate)
library(ggplot2)
# Umwandlung der Daten im deutschen Format tt.mm.jjjj, ohne die Originalspalte zu überschreiben
Altersverteilung_EM_Spieler_2 <- Altersverteilung_EM_Spieler_2 %>%
mutate(GebDat_konvertiert = dmy(GebDat)) # Neue Spalte für konvertierte Daten
# Berechnung des Tages im Jahr für jedes Datum in der neuen Spalte
Altersverteilung_EM_Spieler_2 <- Altersverteilung_EM_Spieler_2 %>%
mutate(Tag_im_Jahr = yday(GebDat_konvertiert)) # yday gibt den Tag im Jahr zurück
# Statistische Berechnungen
# Zusammenfassen der Daten zur Berechnung von Mittelwert, Median, Standardabweichung
statistiken <- Altersverteilung_EM_Spieler_2 %>%
summarise(
Mittelwert = mean(Tag_im_Jahr),
Median = median(Tag_im_Jahr),
Standardabweichung = sd(Tag_im_Jahr),
Differenz_Median_Mean = median(Tag_im_Jahr) - mean(Tag_im_Jahr)
)
# Ausgabe der berechneten Statistiken
print(statistiken)
# Vorbereitung der Daten für einen Boxplot
ggplot(Altersverteilung_EM_Spieler_2, aes(x = "", y = Tag_im_Jahr)) +
geom_boxplot() +
labs(title = "Verteilung der Geburtstage über das Jahr",
y = "Tag im Jahr",
x = "") +
theme_minimal()
# Optional: Speichern des Plots als PNG
ggsave("Boxplot_Geburtstage.png", width = 10, height = 6, dpi = 300)
summary(Altersverteilung_EM_Spieler_2$Tag_im_Jahr)
# 2. Erstellen eines Boxplots für jeden Tag im Jahr, gruppiert nach Land
pp <- ggplot(Altersverteilung_EM_Spieler_2, aes(x = Land, y = Tag_im_Jahr)) +
geom_boxplot() +
stat_summary(fun = mean, geom = "point", shape = 20, size = 3, color = "blue", aes(group = Land)) + # Mittelwert als Punkt hinzufügen
geom_hline(yintercept = 182, linetype = "dashed", color = "red", size = 0.75) + # Korrekt: Linie für den 1. Juli hinzufügen
labs(title = "Verteilung der Geburtstage über das Jahr nach Land",
x = "Land",
y = "Tag im Jahr") +
theme_minimal() +
theme(axis.text.x = element_text(angle = 45, hjust = 1)) +
scale_y_continuous(breaks = seq(1, 365, 30)) # Achsenintervalle für die Y-Achse
# Anzeigen des Plots
print(pp)
# Optional: Speichern des Plots als PNG
ggsave(filename = "Boxplot_Geburtstage_nach_Land_mit_Mean_und_Juli1.png", plot = pp, width = 12, height = 6, dpi = 300)
# 3. Tabelle mit allen Werten pro Land
# Berechnen der statistischen Daten für jedes Land
statistische_daten <- Altersverteilung_EM_Spieler_2 %>%
group_by(Land) %>%
summarise(
Min = min(Tag_im_Jahr),
Lower_Quartile = quantile(Tag_im_Jahr, 0.25),
Median = median(Tag_im_Jahr),
Upper_Quartile = quantile(Tag_im_Jahr, 0.75),
Max = max(Tag_im_Jahr),
Mean = mean(Tag_im_Jahr),
SD = sd(Tag_im_Jahr),
Differenz_Mean_Median = Mean - Median
)
# Anzeigen der berechneten statistischen Tabelle
print(statistische_daten)
# Erstelle eine interaktive Datentabelle und formatiere numerische Werte auf zwei Dezimalstellen
interaktive_tabelle <- datatable(
statistische_daten,
options = list(pageLength = 10, autoWidth = TRUE),
filter = 'top',
rownames = FALSE # Deaktiviere Zeilennummern, falls nicht gewünscht
) %>% formatRound( # Runde und formatiere die numerischen Spalten
columns = c("Min", "Lower_Quartile", "Median", "Upper_Quartile", "Max", "Mean", "SD", "Differenz_Mean_Median"),
digits = 2 # Setze die Dezimalstellen auf zwei
)
# Exportiere die Tabelle als HTML
saveWidget(interaktive_tabelle, 'Statistische_Daten.html', selfcontained = TRUE)
Anhang 3: Verwendete R Pakete
Hier sind die Beschreibungen für die von Ihnen verwendeten R-Pakete:
lubridate: Das Paket lubridate erleichtert die Arbeit mit Datums- und Uhrzeitdaten in R. Es bietet eine Reihe von Funktionen, um Datumszeiten zu parsen, zu manipulieren und zu berechnen, und macht den Umgang mit Zeitzonen und Sommerzeitumstellungen einfacher und intuitiver.
ggplot2: ggplot2 ist ein sehr beliebtes Grafikpaket in R, das auf der Grammatik der Grafiken basiert. Es ermöglicht Benutzern, komplexe und ästhetisch ansprechende Grafiken systematisch zu erstellen. ggplot2 verwendet eine Schicht-basierte Struktur für das Erstellen grafischer Darstellungen und unterstützt eine breite Palette von Diagrammtypen und -stilen.
dplyr: Das Paket dplyr bietet eine Sammlung von Funktionen für die Datenmanipulation in R, die eine intuitive und leistungsfähige Datenbearbeitung ermöglicht. Es ist besonders effizient im Umgang mit Datenrahmen und bietet Funktionen wie filter, arrange, select, mutate und summarise.
tidyr: tidyr ist ein R-Paket zur Datenbereinigung, das dabei hilft, Daten zu “tidy” (aufgeräumten) Formaten zu organisieren. Es bietet Funktionen wie pivot_longer und pivot_wider, die es einfach machen, zwischen langen und breiten Formaten von Datensätzen zu wechseln, und erleichtert so die Datenanalyse und Visualisierung.
DT: Das Paket DT bietet eine R-Schnittstelle für die DataTables-Bibliothek, welche interaktive Tabellen in Webseiten ermöglicht. Es erlaubt es Benutzern, R-Datenrahmen in interaktive, JavaScript-basierte Datentabellen umzuwandeln, die in R Markdown-Dokumenten oder Shiny-Webanwendungen eingebettet werden können.
htmltools: htmltools bietet Funktionen zur Erstellung und Bearbeitung von HTML-Code in R. Es ist besonders nützlich in Kombination mit anderen Paketen wie Shiny, um dynamische Webinhalte zu generieren. htmltools ermöglicht das Erstellen von HTML-Tags, das Kombinieren von Tags zu komplexeren HTML-Strukturen und das Einbetten von externen CSS- und JavaScript-Abhängigkeiten.
Diese Pakete bieten zusammen eine umfassende Suite an Tools für Datenmanipulation, Analyse, Visualisierung und Präsentation in R.



