Veröffentlichungsdatum: 14. Juli 2024

Abstract

Diese Studie untersucht die Altersstrukturen und Talentselektionsstrategien der Teilnehmer der Copa America und der Fußball-Europameisterschaft 2024 durch eine detaillierte statistische Analyse und Clusterbildung der Spielerdaten. Ziel war es, die Verteilung der Geburtstage und die damit verbundenen Talentselektionsstrategien in unterschiedlichen geografischen Kontexten zu vergleichen und mögliche universelle Muster zu identifizieren, die auf eine Standardisierung der Auswahlpraktiken hindeuten könnten. Die Ergebnisse zeigen signifikante Ähnlichkeiten in den Altersstrukturen der Teams beider Kontinente, was auf ähnliche Selektionskriterien und möglicherweise universell anwendbare Entwicklungsphilosophien schließen lässt. Diese Erkenntnisse könnten dazu beitragen, Best Practices in der Talentförderung zu etablieren, die auf bewährten Methoden basieren, die in verschiedenen internationalen Kontexten erfolgreich sind. Sie könnten auch dazu dienen, Diskussionen über mögliche Anpassungen in den Auswahlprozessen anzustoßen, um eine gerechtere und effektivere Entwicklung junger Talente sicherzustellen. Die Studie legt nahe, dass durch die Anwendung fortschrittlicher statistischer Methoden und Clusteranalysen tiefere Einblicke in die Talententwicklungsstrategien gewonnen werden können, die die Grundlage für eine informierte Überarbeitung und Verbesserung der Methoden zur Talentselektion bieten.

Keywords: Talentselektion, Relative Age Effect, Fußball-Europameisterschaft 2024, Copa America, Altersstrukturen, Clusteranalyse, Internationale Fußballturniere, Talententwicklung,  Sportstatistik

1. Einführung

Der Relative Age Effect (RAE) beschreibt ein Phänomen, bei dem Individuen, die in den ersten Monaten eines Auswahljahres geboren wurden, in sportlichen Kontexten systematische Vorteile haben. Dies wird durch die größere physische und psychologische Reife im Vergleich zu ihren jüngeren Altersgenossen innerhalb desselben Jahrgangs erklärt. Frühere Studien haben gezeigt, dass der RAE die Talentidentifikation und -entwicklung in vielen Sportarten beeinflusst, insbesondere im Fußball, wo das Auswahlalter einen kritischen Faktor für die Aufnahme in Eliteprogramme darstellt.

Die vorliegende Studie zielt darauf ab, den Einfluss des RAE auf die Talentauswahl bei zwei bedeutenden Fußballturnieren, der Copa America und der Europameisterschaft 2024, zu analysieren. Durch den Vergleich dieser Turniere erhoffen wir uns ein tieferes Verständnis darüber, wie geografische und kulturelle Unterschiede die Ausprägung des RAE beeinflussen können. Diese Untersuchung ist besonders relevant, da sie Aufschluss darüber geben soll, ob die Selektionsvorteile, die ältere Spieler genießen, universell sind oder von spezifischen regionalen Faktoren abhängen.

Forschungsfragen

1. Vergleich zwischen den Kontinenten: Wie unterscheiden sich die Auswirkungen des RAE auf die Spielerselektion zwischen den Teilnehmern der Copa America und der Europameisterschaft 2024? Ziel ist es, festzustellen, ob es signifikante Unterschiede in der Verteilung der Geburtsmonate gibt, die auf unterschiedliche Ausprägungen des RAE hinweisen könnten.

2. Analyse der Teamstrukturen über Kontinente hinweg: Gibt es Ähnlichkeiten in den Teamstrukturen hinsichtlich des RAE, die unabhängig vom Kontinent sind? Diese Frage untersucht, ob Teams aus verschiedenen geografischen Regionen ähnliche Muster aufweisen, was darauf hindeuten könnte, dass bestimmte Auswahlpraktiken global verbreitet sind.

Durch die Beantwortung dieser Fragen strebt die Studie danach, wertvolle Einsichten für die Gestaltung fairerer und effektiverer Auswahl- und Trainingsmethoden in der globalen Fußballgemeinschaft zu liefern. Die Ergebnisse könnten dazu beitragen, die Praktiken in Sportakademien zu verbessern und eine gerechtere Talentförderung zu fördern.

2 Methoden

Datenerhebung

Für diese Studie wurden die Geburtsdaten der Spieler, die an der Copa America und der Europameisterschaft 2024 teilnahmen, analysiert. Die Daten wurden aus öffentlich zugänglichen Quellen gesammelt, einschließlich offizieller Turnierwebsites und sportstatistischen Datenbanken wie Transfermarkt.de und UEFA.com. Die Datensätze enthielten Informationen über das Geburtsdatum jedes Spielers, aufgeschlüsselt nach Tag, Monat und Jahr.

Datenaufbereitung

Die Geburtsdaten wurden zunächst in eine standardisierte Form (YYYY-MM-DD) überführt und in zwei separate DataFrames für die Copa America und die Europameisterschaft eingetragen. Für die Analysen wurden die Geburtstage in Tageszahlen des Jahres umgerechnet, um eine präzisere Untersuchung der Altersverteilung zu ermöglichen.

Deskriptive Analyse

Für jeden der beiden Turnier-DataFrames wurden deskriptive Statistiken berechnet, darunter Minima, Maxima, Mittelwerte, Mediane, untere und obere Quartile sowie die Standardabweichung der Geburtstage. Diese Statistiken ermöglichten einen ersten Einblick in die Altersstrukturen der Teams und dienten als Grundlage für weiterführende Analysen.

Statistische Tests

Um die Forschungsfragen zu adressieren, wurden verschiedene statistische Tests durchgeführt:

1. T-Test und ANOVA: Zum Vergleich der Mittelwerte der kontinuierlichen Altersvariablen zwischen den Kontinenten wurde ein T-Test verwendet, ergänzt durch eine ANOVA, um die Varianz zwischen den Gruppen zu analysieren.

2. Wilcoxon- und Kruskal-Wallis-Tests: Diese nicht-parametrischen Tests wurden eingesetzt, um die Mediane der Altersverteilungen zu vergleichen, da sie weniger anfällig für Ausreißer sind und keine Normalverteilung der Daten voraussetzen.

Clusteranalyse (k-means)

Um die zweite Forschungsfrage zu untersuchen, wurde eine k-means Clusteranalyse durchgeführt. Die Spielerdaten wurden auf Basis ihrer numerischen Merkmale (Minima, Quartile, Maxima, Mittelwerte, Standardabweichungen und Tag des Jahres) gruppiert. Die Daten wurden zuerst skaliert, um eine gleichmäßige Gewichtung aller Variablen sicherzustellen. Die optimale Anzahl der Cluster wurde über die Methode des Ellbogenkriteriums bestimmt und die Analyse mit verschiedenen Startkonfigurationen wiederholt, um die Stabilität der Cluster zu gewährleisten.

Visualisierung

Zur Visualisierung der Ergebnisse wurden Boxplots für die Mediane sowie Scatterplots für die Clusteranalysen erstellt. Diese Visualisierungen helfen, die Verteilung und Gruppierung der Daten intuitiv zu verstehen und unterstützen die Interpretation der statistischen Tests.

Software

Die Analysen wurden mit der statistischen Software R durchgeführt. Dabei kamen verschiedene Pakete wie `tidyverse` für Datenmanipulation, `ggplot2` für das Erstellen von Grafiken und `ggpubr` für die Publikation der Ergebnisse zum Einsatz.

3. Ergebnisse

3.1        Ergebnisse der ersten Forschungsfrage: Vergleich der Altersverteilung zwischen den Kontinenten

Deskriptive Statistiken

Die deskriptiven Analysen zeigten, dass die Spieler der Copa America im Mittel jünger waren als die Spieler der Europameisterschaft. Die folgenden sind die zentralen deskriptiven Maße für beide Gruppen:

Amerika: 

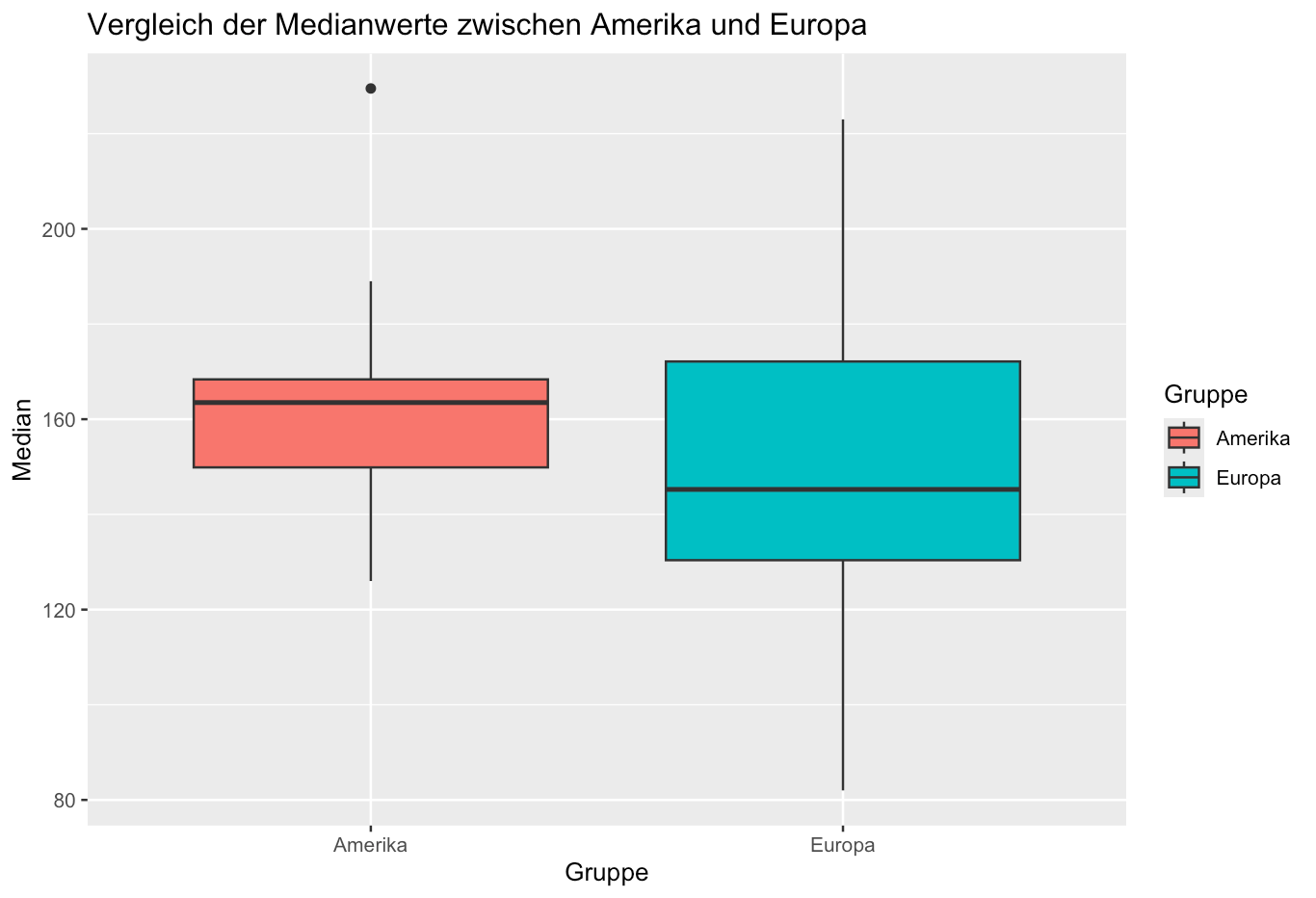
- Median des Alters: 163.5 Tage

- Mittelwert des Alters: 169.54 Tage

- Standardabweichung: 104.51 Tage

Europa: 

- Median des Alters: 148.7 Tage

- Mittelwert des Alters: 161.10 Tage

- Standardabweichung: 103.10 Tage 

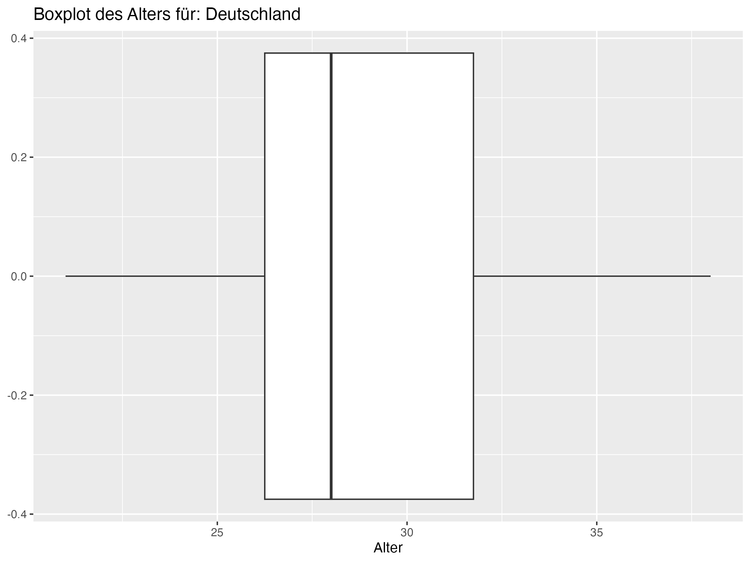
Die Boxplots verdeutlichten, dass die Mediane der Altersverteilung in Amerika leicht höher lagen als in Europa, was auf eine geringfügig ältere Spielerpopulation in Amerika hinweist.

Statistische Tests

T-Test für unabhängige Stichproben:

- Ergebnis: t = 1.6765 , df = 37.203, p-Wert} = 0.102

- Der T-Test zeigte keinen signifikanten Unterschied in den Mittelwerten der Altersverteilung zwischen den Kontinenten.

ANOVA:

- Ergebnis: F = 2.522 , p-Wert = 0.121

- Die ANOVA bestätigte ebenfalls, dass keine signifikanten Unterschiede in den Mittelwerten der Altersverteilung zwischen den Gruppen bestehen.

Wilcoxon-Test:

- Ergebnis: W = 251.5, p-Wert = 0.1032

- Der Wilcoxon-Test zeigte keine signifikanten Unterschiede in den Medianen der Altersverteilung.

Kruskal-Wallis-Test:

- Ergebnis: chi^2 = 2.7006, df = 1, p-Wert = 0.1003

- Ähnlich wie die anderen Tests deutet der Kruskal-Wallis-Test darauf hin, dass keine signifikanten Unterschiede im Median des Alters zwischen den beiden Kontinenten bestehen.

 Die statistischen Tests unterstützen die deskriptiven Befunde, die eine sehr ähnliche Altersverteilung zwischen den Fußballspielern in Amerika und Europa aufzeigen, mit leichten Unterschieden, die jedoch statistisch nicht signifikant sind.

3.2 Ergebnisse der zweiten Forschungsfrage: Suche nach Ähnlichkeiten in den Teamstrukturen unabhängig vom Kontinent

k-means Clusteranalyse

Die k-means Clusteranalyse wurde durchgeführt, um Muster in den Daten zu erkennen, die auf Ähnlichkeiten in den Teamstrukturen über die kontinentalen Grenzen hinweg hinweisen könnten. Die Daten wurden nach den Mindest-, Quartil-, Median-, Mittel- und Standardabweichungswerten der Altersverteilung gruppiert.

 Anzahl der Cluster: 3

Clusterzentren:

Cluster 1: Geringere Mindestwerte und enge Verteilung um niedrigere Alterswerte: Dies bedeutet, dass die Alterswerte der Spieler in diesen Teams tendenziell am unteren Ende der Skala liegen und die Streuung um diesen Wert gering ist. Bolivien, CostaRica, Uruguay, Georgien, Polen, Rumänien, Slowakei, Spanien, Österreich

Cluster 2: Mittlere Alterswerte mit breiterer Streuung und durchschnittlichen Mittelwerten: Dies weist auf eine moderatere Altersverteilung mit mittleren Alterswerten hin. Brasilien, Ecuador, Jamaica, Kanada, Kolumbien, Mexico, Paraguay, Peru, USA, Belgien, Dänemark, England, Frankreich, Portugal, Schottland, Schweiz

Cluster 3: Höhere Alterswerte und breitere Altersverteilung: Dies weist auf höhere Alterswerte und eine größere Streuung in den Alterswerten hin. Albanien, Argentinien, Chile, Deutschland, Italien, Kroatien, Niederlande, Panama, Slowenien, Tschechien, Türkei, Ungarn, Venezuela

Die genauen statistischen Werte der Clusterzentren sind:

Cluster 1:

- Min: 0.8005

- Lower Quartile: 0.5224

- Median: -0.1146

- Upper Quartile: -1.0927

- Max: -0.5441

- Mean: -0.4995

- Standard Deviation: -1.4434

- Differenz Mean-Median: -0.2901 

Cluster 2:

- Min: -0.2360

- Lower Quartile: 0.5285

- Median: 0.6987

- Upper Quartile: 0.6266

- Max: 0.3432

- Mean: 0.8253

- Standard Deviation: 0.3639

- Differenz Mean-Median: -0.3836

Cluster 3:

- Min: -0.2274

- Lower Quartile: -1.0934

- Median: -0.8881

- Upper Quartile: -0.1111

- Max: -0.0985

- Mean: -0.7970

- Standard Deviation: 0.4954

- Differenz Mean-Median: 0.7320 

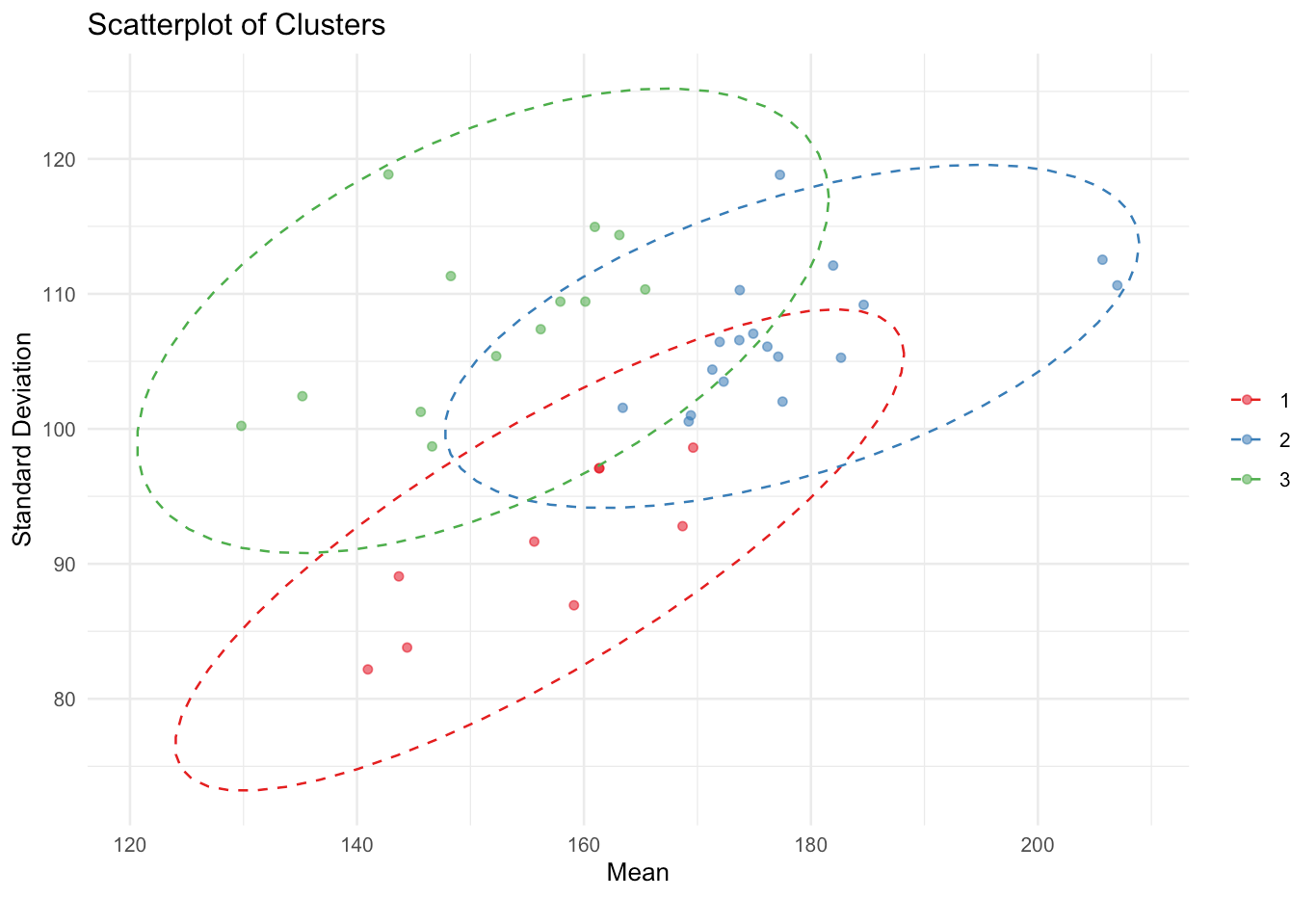
Visualisierung der Cluster

Ein Scatterplot der Cluster zeigt, wie sich die Teams hinsichtlich ihres Alters und der Standardabweichung gruppieren. Die Cluster werden durch verschiedene Farben dargestellt, und Ellipsen um die Cluster verdeutlichen die Streuung und Zentralität der Gruppen. 

Die Zuordnung der Teams zu den Clustern erfolgte ohne Berücksichtigung ihres geografischen Kontexts, was die Untersuchung von strukturellen Ähnlichkeiten unabhängig von kontinentalen Zugehörigkeiten ermöglicht.

4. Diskussion

4.1 Diskussion zur ersten Forschungsfrage: Vergleich der Gruppen Amerika und Europa

Die erste Forschungsfrage konzentrierte sich auf den Vergleich der statistischen Daten zwischen den Teams der Copa America und der Europameisterschaft. Die Analyse umfasste deskriptive Statistiken, T-Tests, Wilcoxon-Tests und ANOVA, um Unterschiede zwischen den Kontinenten zu bewerten.

Deskriptive Statistiken

Die deskriptive Analyse zeigte, dass beide Gruppen unterschiedliche Muster in den statistischen Maßen aufwiesen. Teams aus Amerika tendierten dazu, eine breitere Verteilung in den statistischen Maßen wie Median und Quartilen zu haben. Insbesondere waren die Standardabweichungen und die Unterschiede zwischen Mittelwert und Median in den amerikanischen Teams ausgeprägter, was auf eine größere Heterogenität innerhalb der Teams hindeutet.

T-Test und ANOVA

Die Ergebnisse des T-Tests zeigten keine signifikanten Unterschiede im Mittelwert der Altersverteilung zwischen den Kontinenten (p = 0.102), was darauf hindeutet, dass, obwohl die Teams unterschiedlich strukturiert sein könnten, die zentrale Tendenz ihrer Altersverteilungen ähnlich ist. Die ANOVA bestätigte diese Erkenntnisse mit einem ähnlich hohen p-Wert (p = 0.121), was auf keine wesentlichen Unterschiede im Mittelwert hinweist.

Wilcoxon-Test und Kruskal-Wallis-Test

Der Wilcoxon-Test und der Kruskal-Wallis-Test untersuchten die Medianwerte der Altersverteilungen. Diese nicht-parametrischen Tests sind robust gegenüber nicht-normal verteilten Daten und bieten eine alternative Analyse zu den Mittelwerten. Beide Tests zeigten ebenfalls keine statistisch signifikanten Unterschiede zwischen den Kontinenten (Wilcoxon p = 0.1032; Kruskal-Wallis p = 0.1003), was darauf schließen lässt, dass die zentrale Tendenz der Altersverteilungen ähnlich ist, obwohl die individuelle Variation innerhalb der Teams variiert.

4.2 Diskussion zur zweiten Forschungsfrage: Suche nach Ähnlichkeiten in den Teamstrukturen unabhängig vom Kontinent

Die zweite Forschungsfrage widmete sich der Untersuchung von Ähnlichkeiten in den Teamstrukturen über die kontinentalen Grenzen hinweg, basierend auf den Ergebnissen der k-means Clusteranalyse. Die Clusteranalyse ermöglichte es, Muster innerhalb der kombinierten Daten von Copa America und Europameisterschaft zu identifizieren, die auf ähnliche statistische Profile hinweisen könnten.

K-means Clusteranalyse

Die k-means Clusteranalyse segmentierte die Teams in drei unterschiedliche Gruppen basierend auf verschiedenen statistischen Merkmalen wie Minimum, Quartilen, Maximum, Mittelwert, Standardabweichung und der Differenz zwischen Mittelwert und Median. Diese Gruppierung ermöglichte es, Teams mit ähnlichen Altersverteilungsprofilen zusammenzufassen, unabhängig davon, ob sie aus Amerika oder Europa stammen.

Teams in Cluster 1 zeigen tendenziell niedrigere Mittelwerte und Mediane bei den Geburtstagen der Spieler. Dies deutet darauf hin, dass die Spieler in diesen Teams tendenziell älter innerhalb ihres Jahrgangs sind. Diese Teams könnten eine Strategie verfolgen, die ältere Spieler bevorzugt, um von deren körperlicher und geistiger Reife zu profitieren.

Cluster 2 enthält Teams mit höheren Mittelwerten und größeren Standardabweichungen. Dies deutet auf eine breitere Altersverteilung der Spieler hin. Eine solche Verteilung könnte auf eine ausgeglichenere Talentauswahl schließen lassen, bei der Spieler unterschiedlichen Alters gleichberechtigte Chancen erhalten, was eine integrativere und flexiblere Herangehensweise an die Talentförderung nahelegt.

Teams in Cluster 3 weisen eine gleichmäßigere Altersverteilung über das Jahr hinweg auf, mit weniger extremen Werten in allen statistischen Maßen. Diese gleichmäßige Verteilung könnte eine gerechtere Auswahlpraxis widerspiegeln, die weniger anfällig für den Einfluss des Relative Age Effects (RAE) ist. Dies könnte darauf hindeuten, dass diese Teams eine bewusstere und ausgewogenere Herangehensweise an die Talentauswahl verfolgen, die darauf abzielt, Altersvorteile zu minimieren und allen Spielern gleiche Entwicklungs- und Wettbewerbschancen zu bieten.

5. Schlussfolgerung

Die Ergebnisse der durchgeführten Studien, insbesondere die Clusteranalyse, liefern wertvolle Einsichten in die möglichen Strategien der Talentselektion und -förderung, die von verschiedenen Fußballverbänden weltweit angewendet werden. Durch die Identifizierung von ähnlichen Mustern über Kontinente hinweg scheint es, dass bestimmte erfolgreiche Praktiken universell anwendbar sind, unabhängig von regionalen Unterschieden.

Die Analyse zeigt, dass trotz der kulturellen und strukturellen Unterschiede zwischen den Fußballsystemen in Amerika und Europa ähnliche Muster in den Altersstrukturen der Teams existieren, was auf ähnliche Auswahlkriterien oder Entwicklungsphilosophien hindeuten könnte. Diese Muster könnten darauf hinweisen, dass trotz unterschiedlicher kultureller und struktureller Ansätze in der Talententwicklung und -förderung in Amerika und Europa ähnliche Altersstrukturen bei der Auswahl von Spielern für internationale Turniere bevorzugt werden.

Cluster 1 zeigte Teams mit tendenziell niedrigeren Mittelwerten und Medianen bei den Geburtstagen der Spieler, was darauf hindeutet, dass die Spieler in diesen Teams tendenziell älter innerhalb ihres Jahrgangs sind. Diese Teams könnten eine Strategie verfolgen, die ältere Spieler bevorzugt, um von deren körperlicher und geistiger Reife zu profitieren.

Cluster 2 beinhaltete Teams mit höheren Mittelwerten und größeren Standardabweichungen, was auf eine breitere Altersverteilung der Spieler hinweist. Eine solche Verteilung könnte auf eine ausgeglichenere Talentauswahl schließen lassen, bei der Spieler unterschiedlichen Alters gleichberechtigte Chancen erhalten, was eine integrativere und flexiblere Herangehensweise an die Talentförderung nahelegt.

Cluster 3 umfasste Teams mit relativ gleichmäßiger Altersverteilung über das Jahr hinweg, mit weniger extremen Werten in allen statistischen Maßen. Diese Gruppe könnte eine gerechtere Auswahlpraxis repräsentieren, die weniger anfällig für den Einfluss des Relative Age Effects (RAE) ist.

Diese Erkenntnisse könnten Trainern, Sportwissenschaftlern und Entscheidungsträgern in Sportakademien dabei helfen, ihre Auswahlkriterien und Entwicklungsprogramme zu überdenken, um sicherzustellen, dass sie die bestmöglichen Talente fördern, unabhängig von deren Geburtsmonat oder -quartil. Es legt nahe, dass eine gerechtere und umfassendere Bewertung von Talenten möglicherweise notwendig ist, um die durch den RAE verursachten Verzerrungen zu minimieren.

Zusammenfassend lässt sich sagen, dass, obwohl die Teams aus verschiedenen Kontinenten stammen und möglicherweise unterschiedliche Methoden in der Talentselektion und -förderung anwenden, die grundlegenden Altersstrukturen der ausgewählten Spieler ähnlich sind. Dies unterstreicht die Universalität bestimmter Auswahlkriterien im internationalen Fußball und die mögliche Notwendigkeit, diese Kriterien zu überdenken, um Fairness und Chancengleichheit zu verbessern. Die Anwendung von Clusteranalysen in diesem Kontext bietet eine objektive Methode, um diese Ähnlichkeiten systematisch zu erfassen und zu analysieren, was letztendlich die Grundlage für eine informierte Überarbeitung und Verbesserung der Talententwicklungsstrategien bieten könnte.

Anhang

Anhang 1: R Code

################
#
# 1. deskriptiver Vergleich
# 2. Tests
# 3. k-means Clustering
#
################

################
#
# benötigte Bibliotheken
# library(tidyverse)
# library(ggplot2)
# library(ggpubr)
library(dt)
################



## 1. Erstellen der df
# Erstellen des DataFrames Copa America
daten_amerika <- data.frame(
  Land = c("Argentinien", "Bolivien", "Brasilien", "Chile", "CostaRica", "Ecuador", "Jamaica", "Kanada", "Kolumbien", "Mexico", "Panama", "Paraguay", "Peru", "USA", "Uruguay", "Venezuela"),
  Min = c(1, 13, 1, 15, 15, 9, 6, 7, 13, 3, 28, 11, 1, 9, 20, 2),
  Lower_Quartile = c(72, 74.5, 101.75, 70, 100, 94, 96.5, 94.25, 82, 83.25, 52.5, 91.5, 77, 86.5, 87.5, 59),
  Median = c(136, 171, 171.5, 126, 155.5, 149.5, 229.5, 165.5, 166, 150, 143, 189, 163.5, 167.5, 163.5, 158),
  Upper_Quartile = c(221.25, 214, 229.75, 237, 219.5, 246.5, 304.5, 283.25, 254.75, 273, 259.75, 241, 269, 274.25, 229.75, 250.75),
  Max = c(358, 354, 353, 354, 339, 357, 358, 356, 347, 344, 359, 364, 327, 365, 362, 324),
  Mean = c(146.62, 155.62, 171.31, 165.4, 159.12, 163.42, 205.69, 181.96, 169.42, 173.73, 160.96, 174.92, 172.31, 184.65, 169.62, 157.92),
  SD = c(98.7, 91.65, 104.39, 110.33, 86.93, 101.56, 112.53, 112.1, 101, 110.28, 114.96, 107.05, 103.5, 109.19, 98.61, 109.43),
  Differenz_Mean_Median = c(10.62, -15.38, -0.19, 39.4, 3.62, 13.92, -23.81, 16.46, 3.42, 23.73, 17.96, -14.08, 8.81, 17.15, 6.12, -0.08)
)

# Erstellen des DataFrames für die europäischen Daten
daten_europa <- data.frame(
  Land = c("Albanien", "Belgien", "Deutschland", "Dänemark", "England", "Frankreich", "Georgien", "Italien", "Kroatien", "Niederlande", "Polen", "Portugal", "Rumänien", "Schottland", "Schweiz", "Serbien", "Slowakei", "Slowenien", "Spanien", "Tschechien", "Türkei", "Ukraine", "Ungarn", "Österreich"),
  Min = c(1, 12, 4, 1, 14, 10, 27, 1, 9, 12, 23, 17, 5, 8, 6, 15, 27, 7, 11, 8, 11, 4, 8, 2),
  Lower_Quartile = c(51.25, 93, 45, 104, 84.25, 88, 80, 57.5, 34.75, 53.75, 96.25, 73.25, 99.25, 78.75, 115.75, 55.75, 80, 74, 98.25, 66.75, 57, 90.5, 68.25, 78.25),
  Median = c(82, 147, 116.5, 180.5, 148.5, 159, 149.5, 138.5, 126, 131.5, 127.5, 180.5, 128.5, 171.5, 223, 209.5, 149.5, 136, 174, 131, 100, 176, 143.5, 140),
  Upper_Quartile = c(264.25, 267, 200.5, 238.75, 238.25, 273, 227, 252.75, 253.5, 217.5, 191, 259.5, 188.5, 266, 295, 284, 227, 246.75, 208.25, 240.25, 195.25, 244, 298.75, 204),
  Max = c(361, 357, 335, 363, 364, 354, 352, 354, 330, 345, 318, 348, 305, 343, 354, 357, 352, 337, 329, 364, 364, 350, 326, 354),
  Mean = c(142.77, 177.12, 129.81, 177.5, 169.23, 176.16, 161.35, 156.19, 148.27, 145.62, 140.96, 182.65, 144.42, 173.69, 207, 177.27, 161.35, 152.27, 168.69, 160.12, 135.19, 171.96, 163.12, 143.69),
  SD = c(118.85, 105.35, 100.22, 102.02, 100.55, 106.09, 97.08, 107.38, 111.32, 101.26, 82.18, 105.27, 83.8, 106.57, 110.63, 118.82, 97.08, 105.39, 92.79, 109.43, 102.42, 106.44, 114.36, 89.07),
  Differenz_Mean_Median = c(60.77, 30.12, 13.31, -3, 20.73, 17.16, 11.85, 17.69, 22.27, 14.12, 13.46, 2.15, 15.92, 2.19, -16, -32.23, 11.85, 16.27, -5.31, 29.12, 35.19, -4.04, 19.62, 3.69)
)

# Anzeigen des DataFrames
print(daten_europa)
print(daten_amerika)


## 
## 2.1 Deskriptive Statistken für die beiden Gruppen
# Deskriptive Statistiken für Amerika
summary_stats_amerika <- summary(daten_amerika)
# Deskriptive Statistiken für Europa
summary_stats_europa <- summary(daten_europa)

print(summary_stats_amerika)
print(summary_stats_europa)


## 2.2 Visualisierung der deskriptiven Statistiken der beiden Gruppen
# Kombinieren der Daten mit einem Gruppen-Label
daten_amerika$Gruppe <- 'Amerika'
daten_europa$Gruppe <- 'Europa'
gesamt_daten <- rbind(daten_amerika, daten_europa)

# .html Export der Gesamtentabelle
# Laden des DT-Pakets
library(DT)

# Erstellen des DataTable-Widgets mit gesamt_daten
datatable_widget <- datatable(gesamt_daten, options = list(pageLength = 25))

# Speichern als HTML-Datei
saveWidget(datatable_widget, 'gesamt_daten.html', selfcontained = TRUE)


# Boxplot für Medianwerte
ggplot(gesamt_daten, aes(x = Gruppe, y = Median, fill = Gruppe)) +
  geom_boxplot() +
  labs(title = "Vergleich der Medianwerte zwischen Amerika und Europa", x = "Gruppe", y = "Median")


## 2.3 T-Test
# T-Test auf Mittelwerte
t_test_result <- t.test(Mean ~ Gruppe, data = gesamt_daten)
print(t_test_result)


# 2.4 Wilcoxon-Test auf Medianwerte
wilcox_test_result <- wilcox.test(Median ~ Gruppe, data = gesamt_daten)
print(wilcox_test_result)


# 2.5 Vergleich der unteren Quartile
wilcox_test_lower_quartile <- wilcox.test(Lower_Quartile ~ Gruppe, data = gesamt_daten)
print(wilcox_test_lower_quartile)


# 2.6 ANOVA für den Mittelwert
anova_result <- aov(Mean ~ Gruppe, data = gesamt_daten)
summary(anova_result)


# 2.7 Kruskal-Wallis-Test für den Median
kruskal_test <- kruskal.test(Median ~ Gruppe, data = gesamt_daten)
print(kruskal_test)

#### 3. k-means Clusteranalyse
# Angenommen, Ihr kombinierter DataFrame heißt gesamt_daten

# Auswahl der relevanten Spalten (numerische Variablen für das Clustering)
clustering_data <- gesamt_daten %>% 
  select(Min, Lower_Quartile, Median, Upper_Quartile, Max, Mean, SD, Differenz_Mean_Median)

# Skalieren der Daten
clustering_data_scaled <- scale(clustering_data)

# K-means Clustering durchführen
set.seed(123)  # Für Reproduzierbarkeit der Ergebnisse
k <- 3  # Anzahl der Cluster
kmeans_result <- kmeans(clustering_data_scaled, centers = k, nstart = 25)

# Ausgabe der Clusterzentren
print(kmeans_result$centers)

# Hinzufügen der Clusterzuweisungen zu den ursprünglichen Daten
gesamt_daten$cluster <- kmeans_result$cluster


# Erstellen des Scatterplots
scatter_plot <- ggplot(gesamt_daten, aes(x = Mean, y = SD, color = as.factor(cluster))) +
  geom_point(alpha = 0.6) +  # Punkte halbtransparent machen
  stat_ellipse(type = "norm", linetype = "dashed", level = 0.95) +  # Ellipsen um Cluster
  scale_color_brewer(palette = "Set1") +  # Farbpalette für Cluster
  labs(title = "Scatterplot of Clusters", x = "Mean", y = "Standard Deviation") +
  theme_minimal() +
  theme(legend.title = element_blank())  # Legendentitel entfernen

# Anzeigen des Plots
print(scatter_plot)